统计学(一) 概率及概率分布
本文最后更新于:2023年2月28日 下午
1. 试验、事件和概率
1.1 基本概念
随机试验
对一个或多个试验对象进行一次观察成测量的过程,称为一次试验 (experiment)。而其中可在相同条件下重复进行,知道试验的所有可能结果,不确定试验的确切结果的为随机试验。
随机事件
试验的结果称为事件/随机事件 (event),常记作大写字母。
- 简单事件 (simple event):不能被分解成其它事件组合的事件。
- 必然事件:
- 不可能事件:
样本空间
样本空间 (sample space):试验中所有可能结果(简单事件)的集合,记作 。
样本点 (sample space):样本空间中每一个特定的试验结果,记作 。

随机变量
随机变量 (random variable):试验中所有可能结果的数值型描述,即随机试验样本空间上的单值实数函数(将样本点映射至实数)。随机变量通常记作大写字母 ,随机变量的取值用相应的小写字母 表示。
- 离散型随机变量 (discrete random variable):只能取有限个或可数个值的随机变量。
- 连续型随机变量 (continuous random variable):可以取一个或多个区间中任何值的随机变量。
概率
概率 (probability):度量事件发生的可能性,介于-间,记作 。通常用多次试验下,事件发生的次数占总试验次数的比例逼近。

1.2 条件概率
随机事件的关系
| 事件类型 | 符号 | 含义 | 概率性质 |
|---|---|---|---|
| 子事件 | 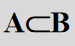 |
事件A发生必然导致事件B发生 | 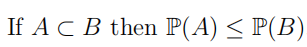 |
| 和事件/事件的并 (union) |
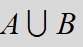 |
事件A与事件B至少有一个发生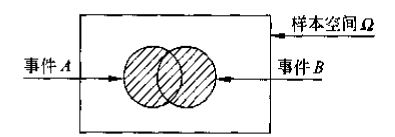 |
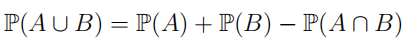 |
| 积事件/事件的交 (intersection) |
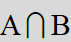 |
事件A与事件B都发生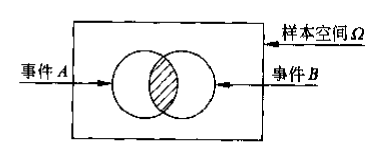 |
|
| 差事件 | 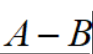 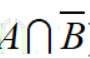 |
事件A发生而事件B不发生 | 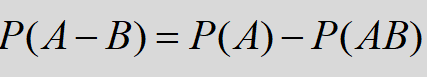 |
| 互斥事件 (mutually exlusive events) |
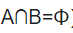 |
事件A与事件B不可能同时发生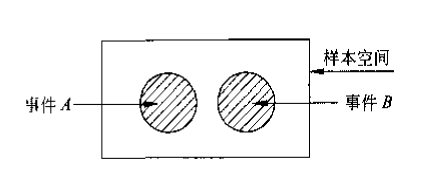 |
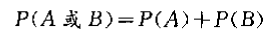 |
| 补事件/对立事件 (complement) |
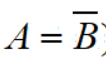 |
事件A不发生的事件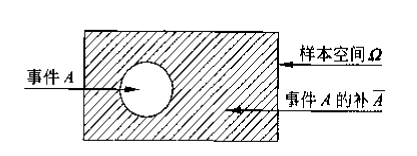 |
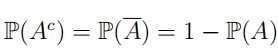 |
条件概念与计算公式
条件概率 (conditional probability):已知事件发生的条件下事件发生的概率,记作 。
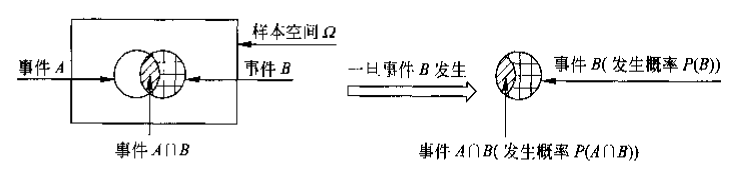

两个事件的交发生的概率称为联合概率 (Joint probability),记作 ;
单个事件的发生概率称为边际概率 (marginal probability),记作。
独立事件 (independent events):互不影响发生的事件,即。
概率的乘法公式(multiplication law):
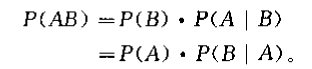
其中,对于独立事件有,
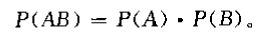
全概率公式 (The Partition Theorem):将相对复杂的事件分解成可由乘法公式计算概率的多个和事件。
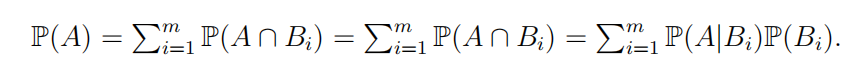
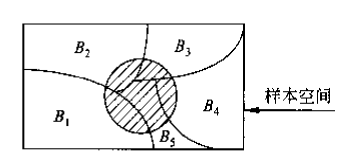
贝叶斯公式 (Bayes’ Theorem):
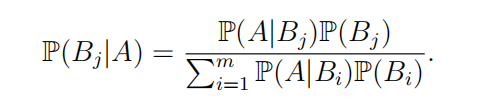
例题

理解题意
:当第i枚硬币被选中时,每一次抛硬币正面朝上的概率(每一次都是概率相等的独立事件)
:当第一次抛硬币正面朝上时,第 枚硬币被选中的概率
三公式运用

2. 随机变量的概率分布
2.1 离散型随机变量的概率分布
期望与方差
引入数学期望 (expected value)和方差以概括性度量离散随机变量的分布特征。
离散型随机变量 的数学期望 :
数学期望是随机变量所有可能取值的加权平均数,以取值的概率为权数。
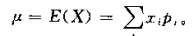
离散型随机变量 的方差 :
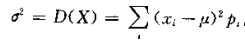
概率质量函数
概率质量函数 (probability mass function, pmf):离散型随机变量在各特定取值上的概率。
离散分布
伯努利随机变量 Bernoulli random variables:
| 分布类型 | 表示 | 释义 | pmf | E(X) | Var(X) |
|---|---|---|---|---|---|
| 两点分布/伯努利分布/0-1分布 | 伯努利试验:只有两种可能结果的随机试验 两点分布即以 次成功概率为 的伯努利试验成功的次数为离散变量 对应的概率分布 |
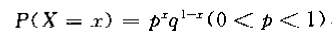 |
|||
| 二项分布 (binomial distribution) | 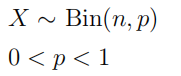 |
二项分布即以 次成功概率为 的伯努利试验成功的次数为离散变量 对应的概率分布 每次试验概率相等,即为重复抽样 |
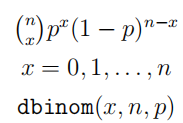 |
||
| 超几何分布 (hypergeometric distribution) | 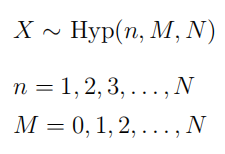 |
超几何分布即以从含有个目标样本的 个样本的总体中随机不放回的 次抽取试验中目标样本的数量为离散变量 对应的概率分布 | 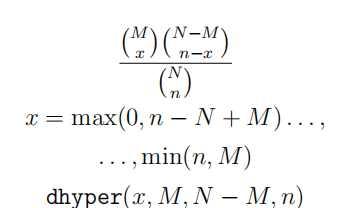 |
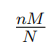 |
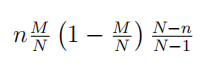 |
| 泊松分布 (Poisson distribution) | 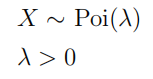 |
泊松分布即以一定时间段或一定空间区域或其他特定单位内某一事件出现的次数为离散变量 ,以为均值对应的概率分布 二项分布的极限分布(极大,极小), |
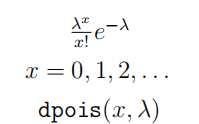 |
||
| 负二项分布 | 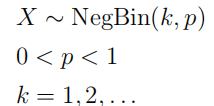 |
负二项分布即以一系列成功概率为 的伯努利试验成功次数为时的失败次数为离散变量 对应的概率分布 | 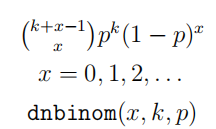 |
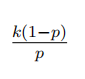 |
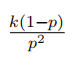 |
| 几何分布 | 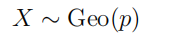 |
几何分布即以一系列成功概率为 的伯努利试验成功次数为时的失败次数为离散变量 对应的概率分布 | 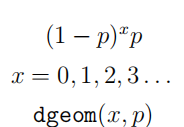 |
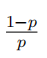 |
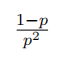 |
离散分布间关系
离散分布类型相同的随机变量之和的离散分布类型
Binomial:
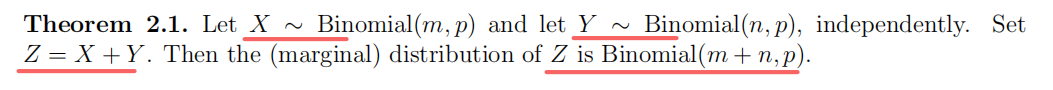
Poisson:
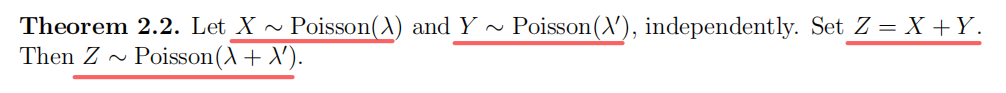 NegBin:
NegBin: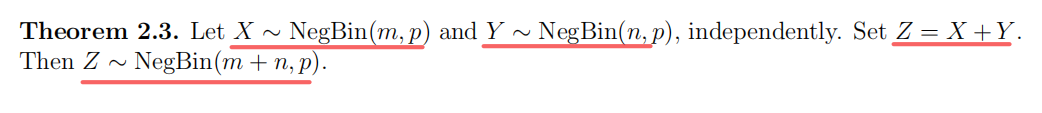 Geometric:
Geometric:

随机变量之和的条件分布
则
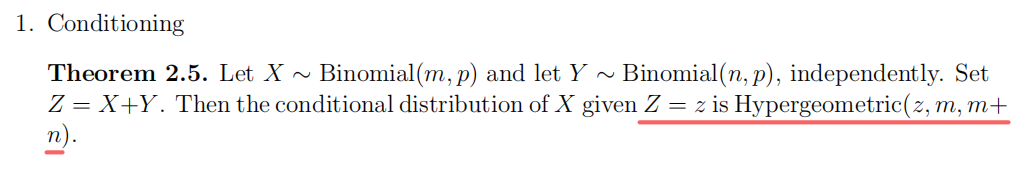
则
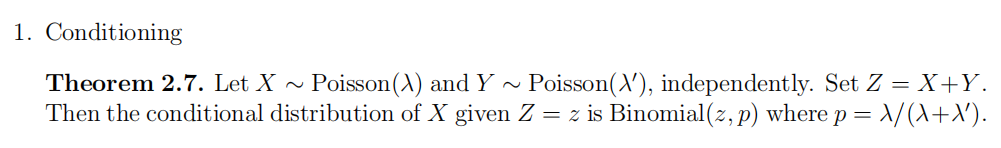
变量趋于极限的离散分布


各离散分布间关系
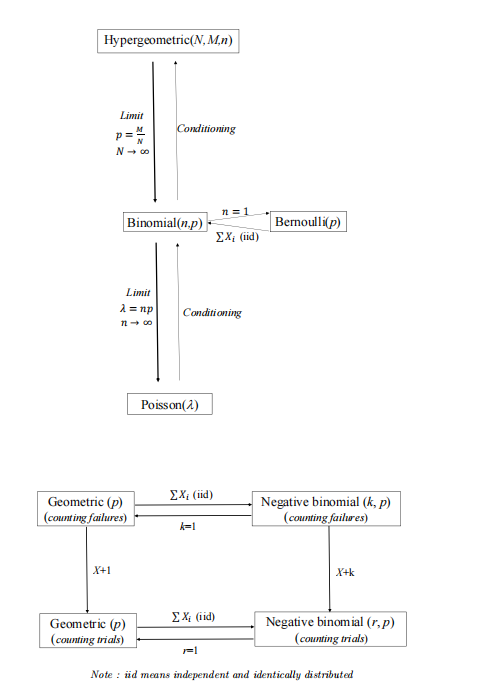
2.2 连续型随机变量的概率分布
概率密度函数
连续型随机变量在特定取值处概率为0,必须在某一区间内考虑相应的概率问题。
概率密度函数 (probability density function, pdf):给出代表某一或多个区间中的任意数值的连续型随机变量 某一特定值处的函数值,曲线在给定区间围成的面积代表在该区间内取值的概率,,记作 。
累积分布函数
累积分布函数/分布函数 (cumulative distribution function, cmf):概率密度函数的积分,描述某随机变量 的概率分布。
连续分布
| 分布类型 | 表示 | 释义 | E(X) | Var(X) | |
|---|---|---|---|---|---|
| 正态分布 (normal distribution) | 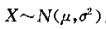 |
正态曲线是以为峰值对称的钟形曲线 确定正态曲线在实数轴的水平位置; 确定正态曲线的陡峭程度(越小越陡峭) 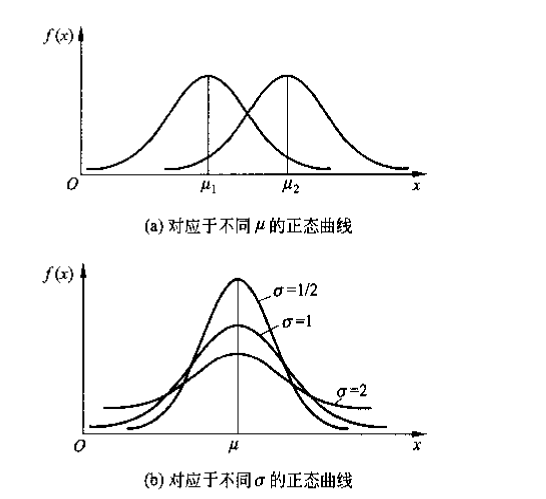 |
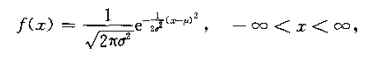 |
||
| 标准正态分布 (standard normal distribution) | 的正态分布 | 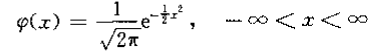 |
正态分布转化为标准正态分布:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!