决策树算法原理及实现
本文最后更新于:2023年2月28日 下午
1. 决策树概述
决策树是一种树形结构,分为分类树和回归树两种:
- 分类树对离散变量决策,输出是样本的分类结果
- 回归树对连续变量决策,输出是样本的预测结果 (实数)
决策分类树是将连续属性离散化后,投入决策分类树判断。
决策树由下面几种元素构成:
-
根节点
包含样本全集
-
内部节点
每个节点包含一个父节点的样本子集,对应一个特征测试
-
叶节点
决策结果
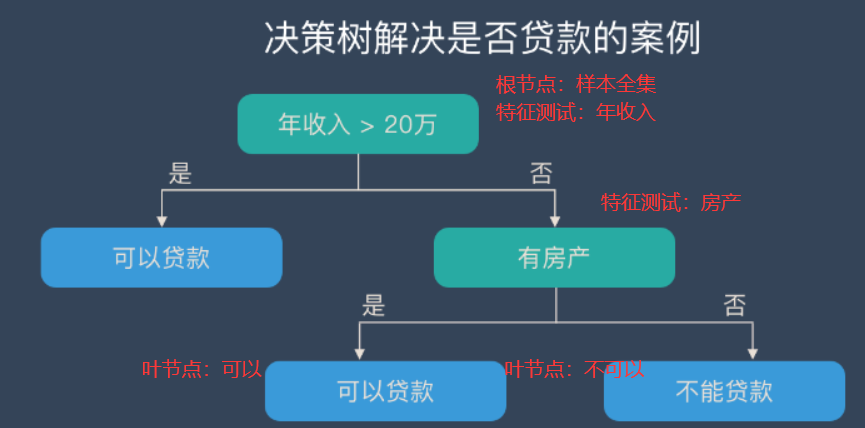
决策树学习自根节点从上至下递归地生成子节点,直至全部子节点为叶节点。
每一个节点处包含一个样本集,需要进行特征选择,根据选定特征对样本集进行特征测试划分为样本子集给其子节点,直至全部子节点为叶节点递归返回。

-
特征选择
从训练集的特征中选择一个特征作为当前节点的分裂标准,特征选择的标准对应不同的决策树生成算法
特征测试分裂样本集时,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,这是各类决策树算法的依据
-
特征测试
将样本集根据选定特征的不同取值,划分为不同样本子集给其子节点
-
递归返回
- 当前结点包含的样本全属于同一类别, 无需划分
- 当前所有样本在所有属性上取值相同,或是属性集为空,无法划分
- 当前结点包含的样本集合为空,不能划分
2. 决策树生成算法
2.1 ID3
Iterative Dichotomiser 3 (迭代二叉树3代)
信息增益
信息增益
使用 ID3 算法进行决策树特征选择中,信息增益越大,则该特征越重要。
某特征 对于某样本集 的信息增益由 (该特征)信息熵 - (该特征)条件熵之和 计算得到:

特征选择,即选择信息增益最大的特征:
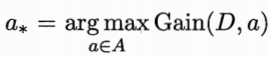
信息熵

算法实例和缺陷
算法实例
以西瓜书中例子加以理解:
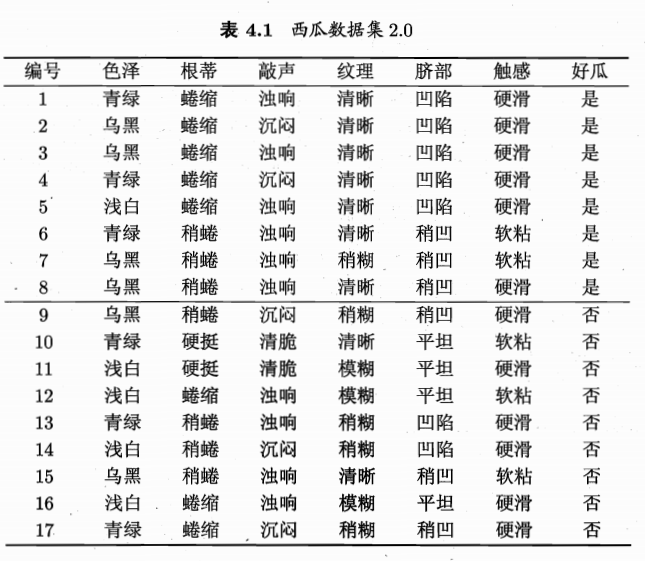
-
计算总信息熵
根据 分类结果——是否是好瓜 得到信息熵
样本共类:好瓜、坏瓜,在样本集中所占比例:
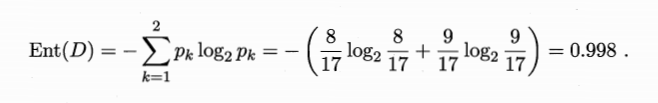
-
计算各特征信息增益,选取信息增益最大者作为分类标准
当前特征集合
{色泽,根蒂,敲声,纹理,脐部,触感},以色泽为例-
,其中 ,则 信息熵为
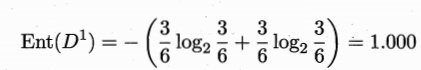
-
,其中 ,则 信息熵为
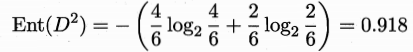
-
,其中 ,则 信息熵为
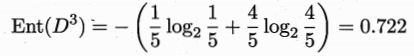
则该特征信息增益为
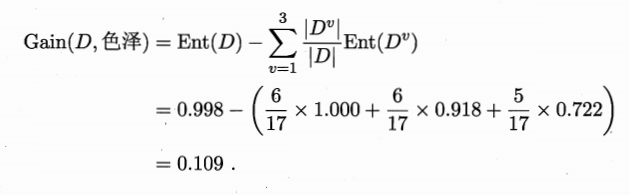
类似计算当前节点所有特征的信息增益

因此,选取信息增益最大的特征
纹理为第一个特征测试的分类标准,得到三个子节点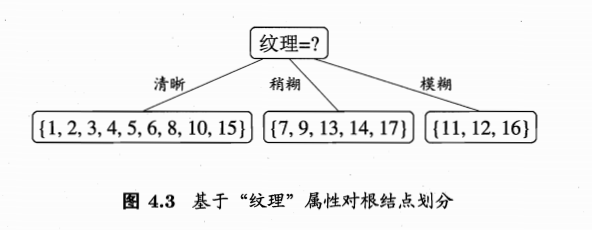
对每处子节点迭代上述过程,直到所有子节点均为叶节点。
-
算法缺陷
-
只能用于处理离散特征,不能处理连续特征
-
无剪枝策略,易出现过拟合
-
信息增益对可取值数目较多的属性有所偏好
上例西瓜中,若
编号也作为一种特征,则该特征信息增益为0.998
2.2 C4.5
信息增益率
信息增益率
每个特征信息增益与属性熵之比
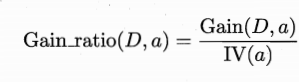
使用 C4.5 算法进行决策树特征选择中,信息增益率越大,则该特征越重要。
属性熵
对于每个属性,其可取值数目越多( 越大),属性熵( 越大)
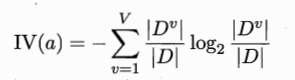
上例西瓜中,
- ,
算法优点和缺陷
算法流程
与ID3大致相同,改为由信息增益率判断分裂标准
算法优点
- 可处理连续值
算法缺陷
- 信息增益率对可取值数目较少的属性有所偏好
2.3 CART
Classification and Regression Tree
基尼系数
基尼系数
基尼系数由基尼值算得。
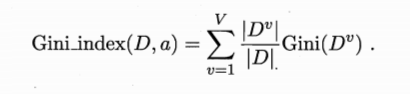
使用 CART 算法进行决策树特征选择中,基尼系数越小,则该特征越重要。在候选特征集合中,选择使划分后基尼系数最小的特征。
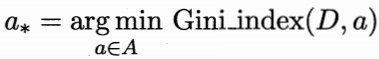
基尼值
反映了从数据集 中随机抽取 两个样本,其类别不一致的概率。基尼值越小,数据集纯度越高 (决策树分支节点包含的样本尽可能属于同一类别) 。
若样本集合 中第 类样本所占的比例为 :

3. 连续属性离散化
连续属性离散化,并计算信息增益:
-
选择划分点
-
将样本集 中连续属性 出现的所有取值从小到大排序,记为
-
对连续属性 ,计算划分点集
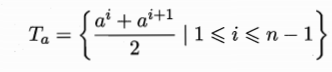
-
基于划分点集 中的每一个划分点 ,将集合划分为不大于 的元素集 ,大于 的元素集
相当于离散特征中,根据特征 的取值将样本集 划分为样本子集
-
-
计算信息增益
-
计算基于划分点
t二分后,样本集D的信息增益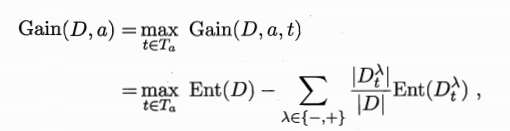
-
以西瓜密度的离散化为例:
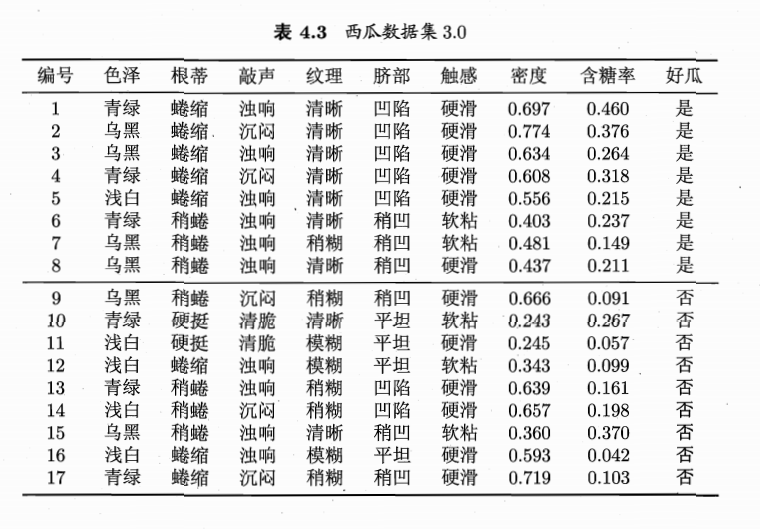
-
将样本中出现的密度取值从小到大排列
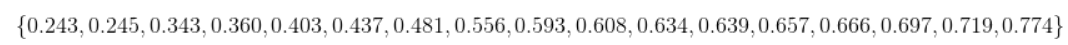
-
计算相邻元素的中位数得到划分点集
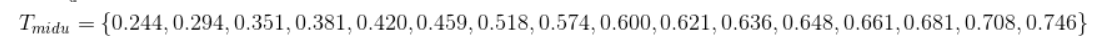
-
计算不同划分点 处的信息增益
① 时:

② 时:
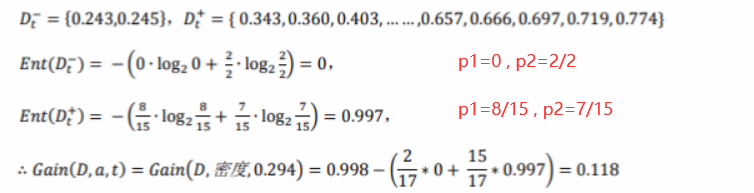
… …
计算出所有的 ,选取信息增益最大的划分点。
本例中为 ,时 最大,则取为该属性信息增益值。

计算所有特征的信息增益,选取信息增益最大的特征为本次特征测试的划分特征。
4. 决策树的剪枝
为防止分支过多决策树过拟合,我们采用剪枝(pruning)策略提高决策树泛化能力
-
预剪枝(pre-pruning) : 在构造决策树的过程中,自上而下对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分,并将当前结点标记为叶结点;
-
后剪枝(post-pruning) : 决策树构造完毕后,自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能提升泛化性能,则将该子树替换为叶结点
3.1 预剪枝
以西瓜为例:
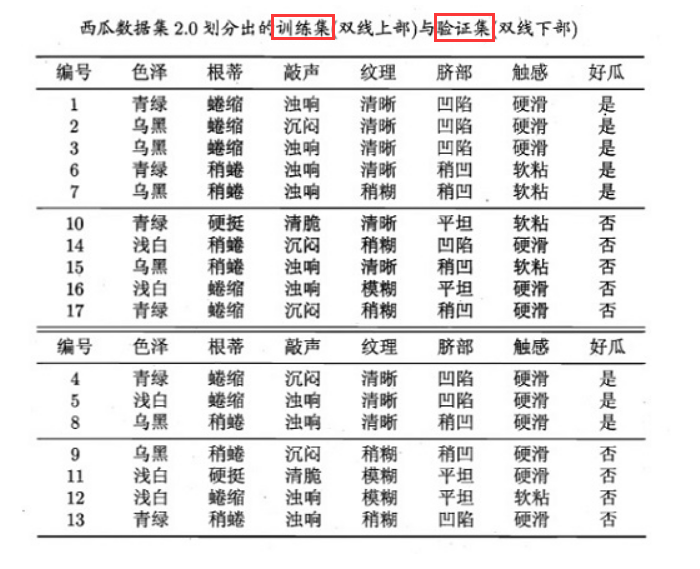
- 划分训练集、验证集后,计算各属性信息增益

- 选取信息增益最大的特征,本例中为脐部和色泽,我们以脐部为分裂准则可以得到
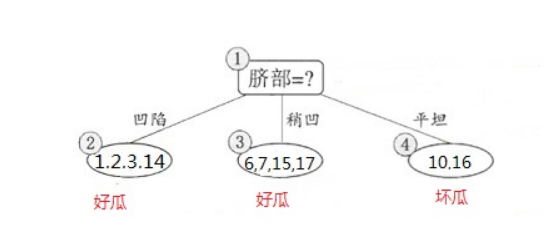
-
判断该节点划分前后泛化性能 (验证集上的准确率)
-
划分前
将该结点标记为叶节点,将节点处所有验证集样本分类结果标记为训练集中含样本数最多的类别 好瓜(本例中训练集两种分类结果含样本数相同,可任选)
准确率
3/7 = 42.9%(或标记为坏瓜4/7 = 57.1%) -
划分后
验证集
{4, 5, 8, 11, 12}判断准确准确率
5/7 = 71.4%
-
划分后准确率提升,预剪枝策略为划分
-
以此类推,在构造决策树的过程中使用预剪枝策略可以得到
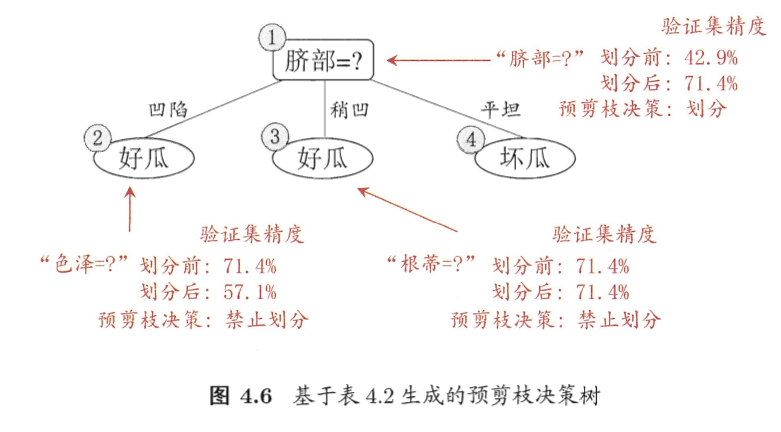
3.2 后剪枝
以构建好的西瓜决策树为例:
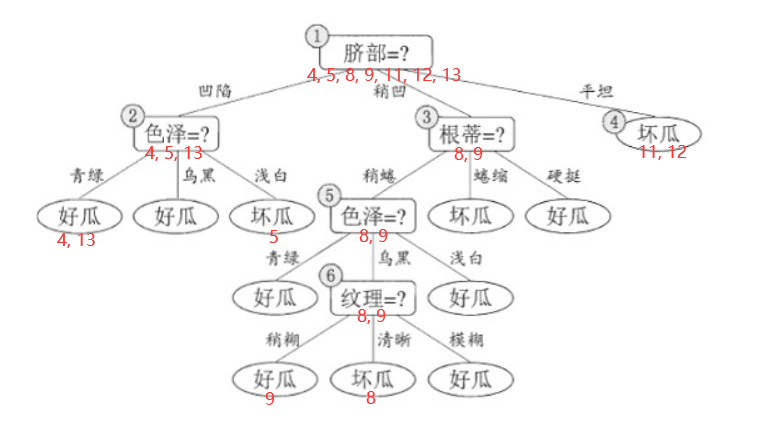
- 自顶向下地排查结点是否需要剪枝,则第一个结点为⑥
-
剪枝前
验证集
{4, 11, 12}判断准确准确率
3/7 = 42.9% -
剪枝后
验证集
{4, 8, 11, 12}判断准确准确率
4/7 = 57.1%
剪枝后准确率提升,后剪枝策略为剪枝
-
以此类推,在决策树构建完成后使用后剪枝策略可以得到
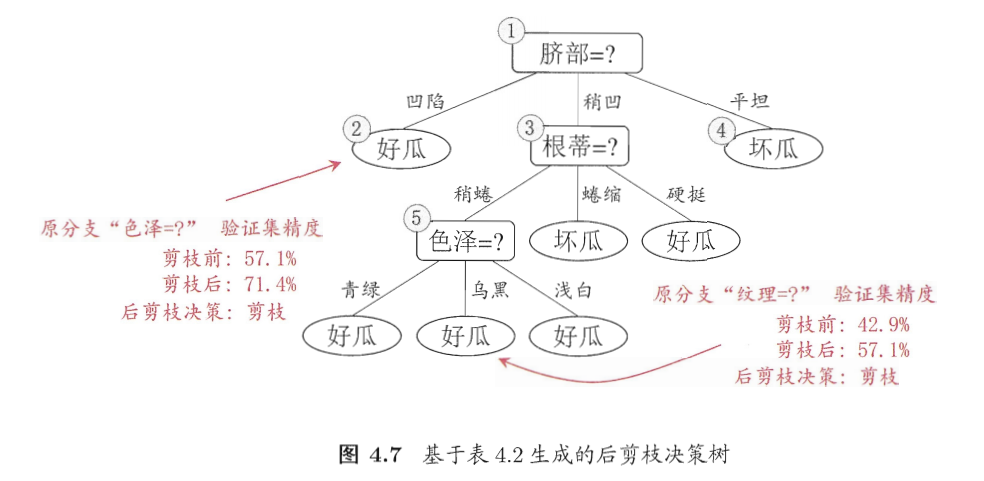
5. sklearn实现决策树
库: sklearn.tree
-
分类器:
DecisionTreeClassifier1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier() # 创建实例
"""
DecisionTreeClassifier参数
criterion:{“gini”, “entropy”}, default=”gini”
=> 分裂特征选择,分别对应基尼系数(CART), 信息增益(ID3)
max_depth:int, default=None
=> 决策树最大深度
min_samples_leaf:int or float, default=1
=> 样本数目少于此,终止分支
min_impurity_decreasefloat, default=0.0
=> 信息增益阈值
"""
clf = clf.fit(data_train, target_train) # 训练,输入为训练集样本和训练集结果
classfier = clf.predit(data_test) # 分类,输入为测试集样本
score = clf.score(data_test, target_test) # 准确率
库: graphviz
实现决策树可视化
1 | |
参考资料
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!