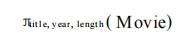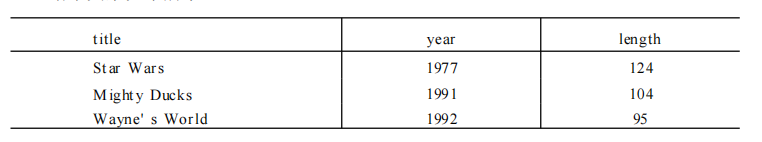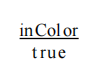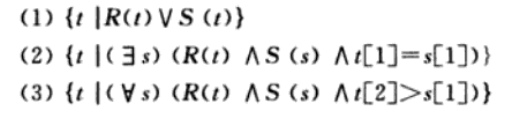数据库(一) 关系模型

1. 数据库概述

术语	释义
数据库系统 database system	DBMS + DBA + DB + DB applications + development tools + users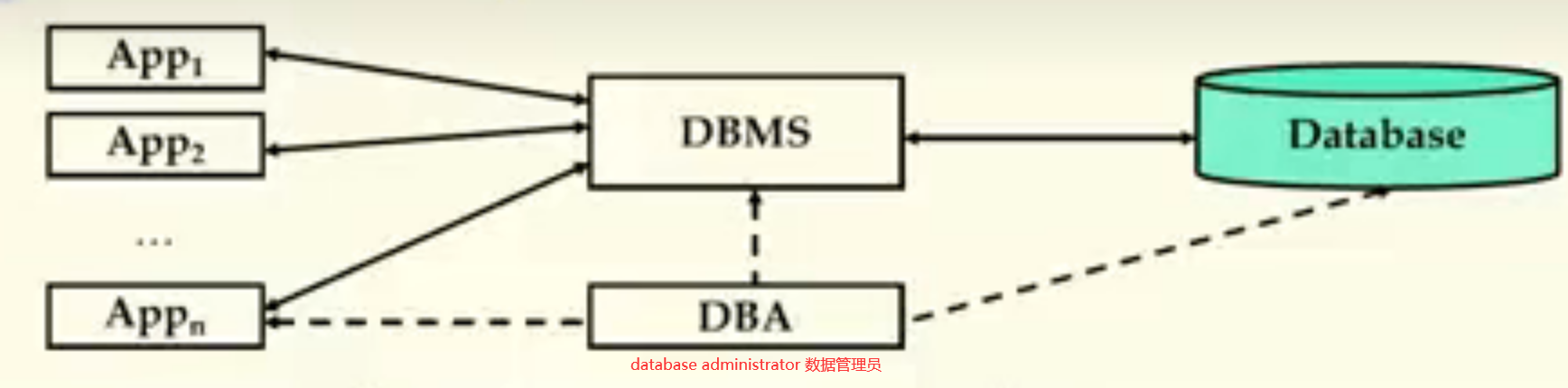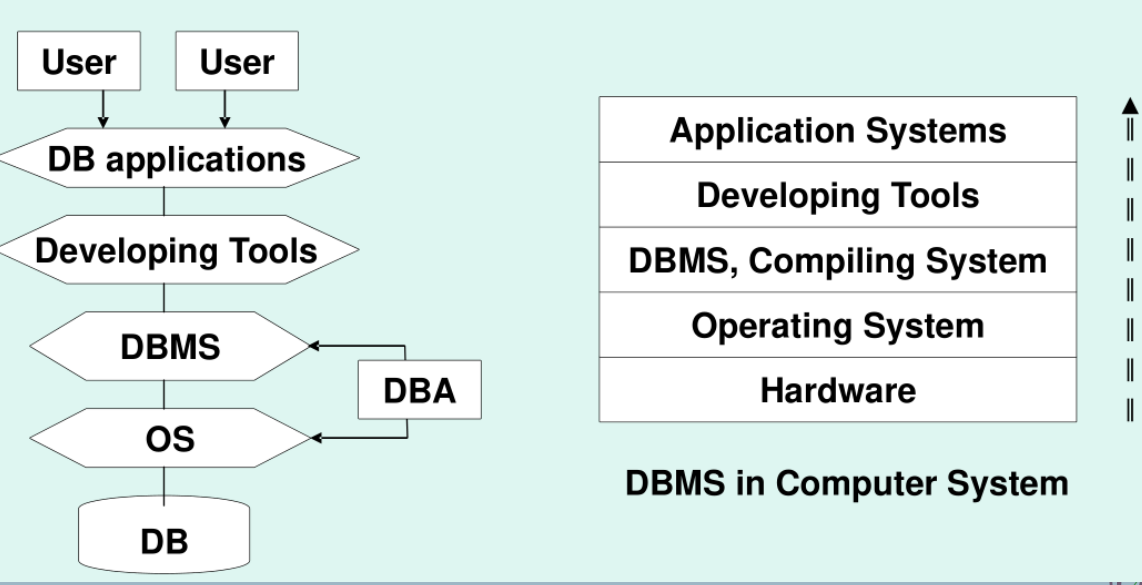
数据库 database	大型集成数据容器 a collection of interrelated data, stored in systems as files.
数据库管理系统 database management system,DBMS	操作数据库的软件 A collection of programs that enables you to store, modify, and extract information from a database.
结构化查询语言 structured query language,SQL	与数据库通信的语言
数据模型 data model	数据的组织方式
数据模式 schema	数据模型的实例 根据抽象级别分为3级模式
物理/存储/内模式 physical/internal schema	描述数据的存储结构
概念/逻辑模式 （简称 模式）conceptual/logic schema	描述数据的逻辑结构
外模式/视图 external schema/view	数据展现的形式 由于对数据的保密要求，根据不同用户的不同需求不同，改变其看到的数据的外模式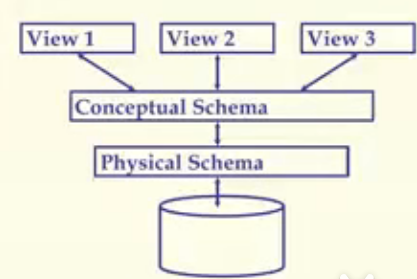

2. 数据模型

数据模型要素

• 数据结构

  数据模型的基础，描述数据的类型、内容、性质以及数据间的联系等

• 数据操作

  相应的数据结构上的数据的操作类型和操作方式

• 数据约束

  相应的数据结构上的数据的制约和依存关系

基本数据模型

层次模型

层次模型是最先出现，通过树形结构表示实体间关系的数据模型。

层次模型中最基本的数据关系是双亲子女关系(parent-child relationship, PCR)，可实现记录型(record type)间”一对一(1:1)“、“一对多(1:n)”关系的描述。

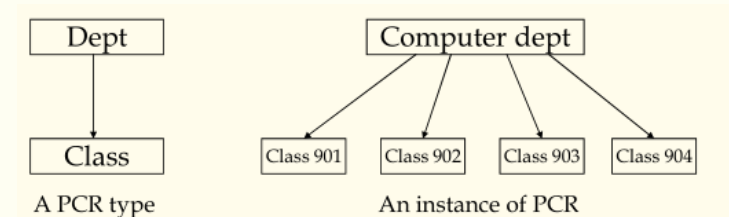
引入虚拟记录(virtual record)描述“多对多(m:n)”关系，并避免冗余。

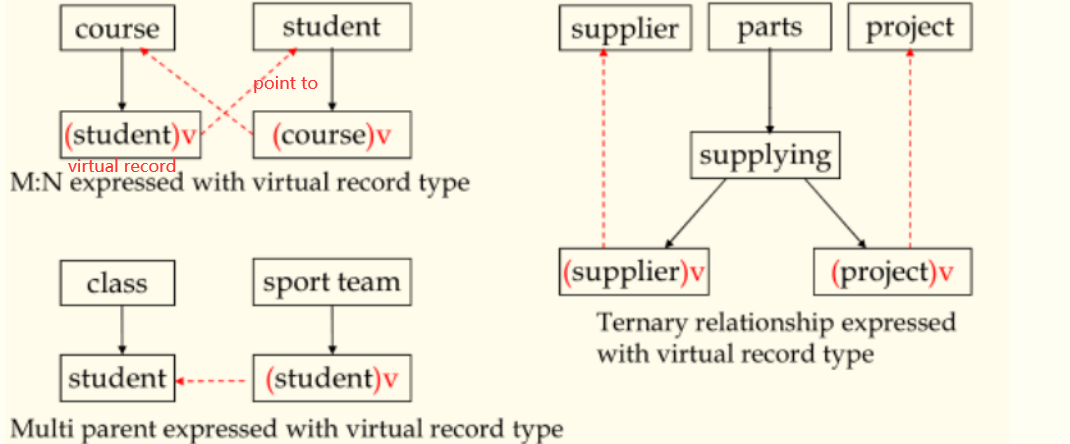
如左上图中，课程和学生之间建立了一个PCR，表示一门课程可以有多个学生选择(1:n)，但孩子节点中的学生类型是虚记录(virtual record)，存储一个指针，指向真正的学生类型的值。

类似的，建立学生和课程之间的PCR则表示一个学生选择的多门课程(1:n)，孩子节点中的课程类型是虚记录，存储一个指向真正的课程类型的值的指针。从PCR角度来看，黑箭头树型结构得到了保持。

网状模型

网状模型基于层次模型，通过有向图表示实体间关系的数据模型。

网状模型使用系(set)描述记录(record type)间“一对多(1:n)”关系，其中“1”方为主记录(owner)，“n”方为子记录(member)。通常使用链表存储。

引入链接记录(LINK record)描述“多对多(m:n)”关系。

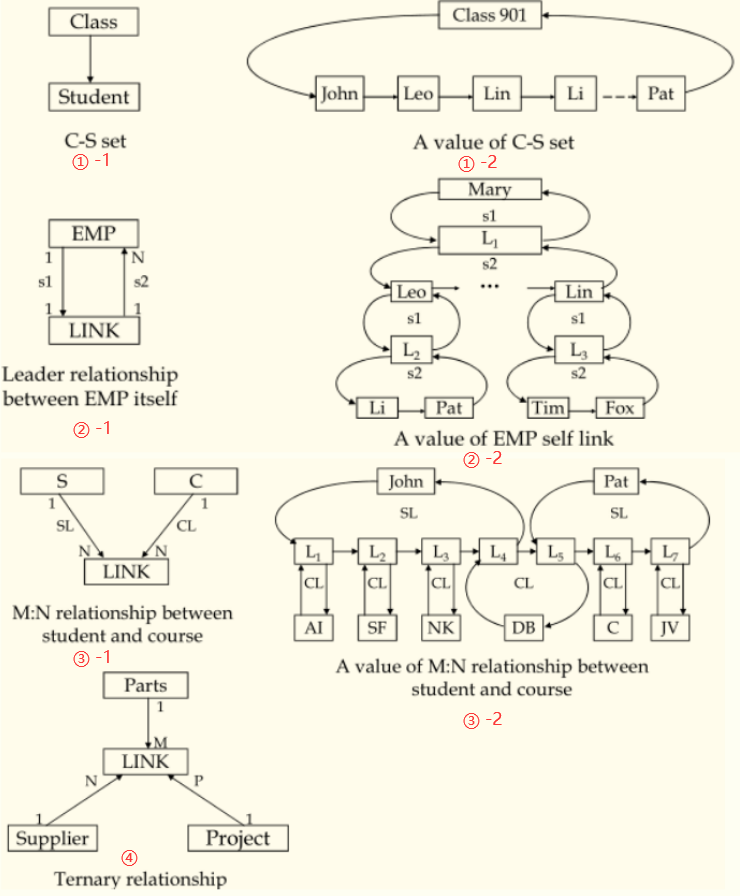
如图 ①-1中，建立了一个以课程为主记录(owner)、学生为子记录(member)的系(set)(1:1)，表示一个班级里有多个学生(1:n)。这个系的实际结构是以主记录为表头的链表(图 ①-2)。对这个班级的学生进行查询即遍历这个链表。

如图 ②-1中，为表达雇员和雇员之间的领导和被领导的关系，需要建立雇员这个类型中的自连接。引入链接记录(LINK record)作为领导雇员的链接，链接被领导的雇员。先建立以雇员类型为主记录、链接记录(LINK record)为子记录的系s1(1:1)，再建立以链接记录(LINK record)为主记录、雇员类型为子记录的系s2(1:n).每一个系对应一个链表，形成链表的嵌套(图 ②-2)。

如图 ③-1中，为表达学生和课程间的”多对多“关系(m:n)，建立两个以学生类型、课程类型为主记录、链接记录(LINK record)为子记录的系SL、CL(1:n)，合成表示(图 ③-2)。

关系模型

关系模型是当前主流，通过二维表格结构表达实体实体间关系的数据模型。

• 关系代数

• SQL语言

其他数据模型还有ER模型、面向对象的数据模型、时态数据模型、空间数据模型、XML等。

3. 关系模型

相关概念

笛卡尔积 (Cartesian Product)

关系的概念是建立在笛卡尔积概念的基础上的。

给定一组域 $D_1,D_2,...,D_n$，这 $n$ 个域的笛卡尔积为，集合中的每一个元素 $(d_1,d_2,...,d_n)$ 是一个 $n$ 目元组(n-tuple)，每一个元素中的 $d_i$ 是一个分量 (Component)：

$D_1 × D_2 × … × D_n ＝ {(d_1,d_2,…,d_n)|d_i∈D_i, i＝1,2,…,n} $

因此，笛卡尔积表示的是一个二维表。表中每一行对应一个元组；每一列对应一个属性，来自同一域。

关系 (Relation)

满足一定语义的$D_1 × D_2 × ... × D_n$ 的子集为域 $D_1,D_2,...,D_n$ 的关系。

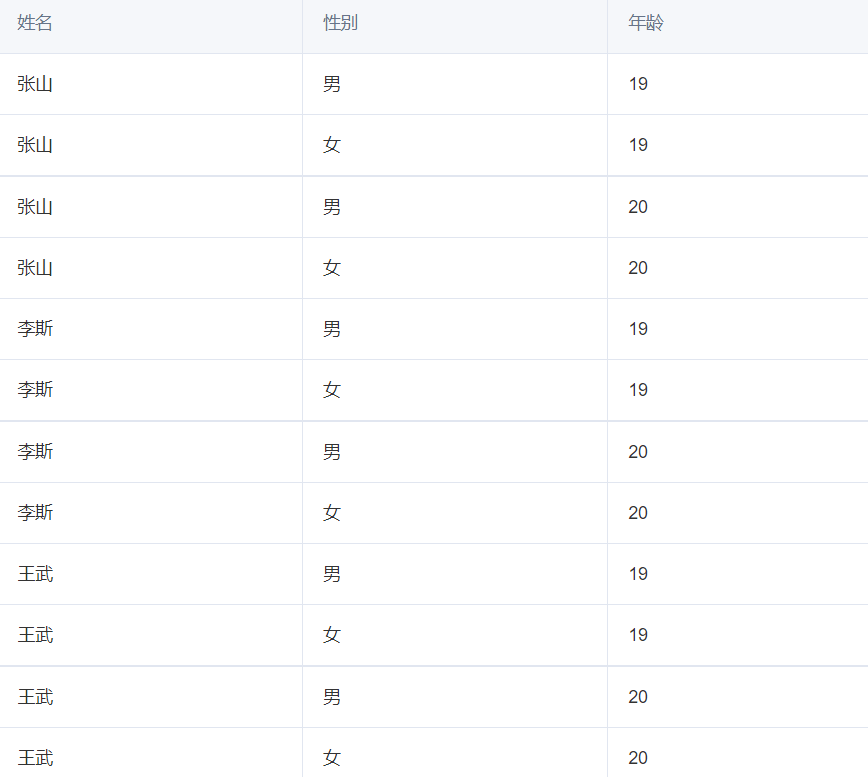
如 $D_1$为学生集合= {张山，李斯，王武}；$D_2$为性别集合= {男，女}；$D_3$为年龄集合= {19，20}，则$D_1 × D_2 × D_3$ 有12个元组：

关系模式 (Relation Schema)

对关系的描述。

可以表示为：

• R(U,D,dom,F)

  R：关系名

  U：该关系的属性集合

  D：属性的域

  dom：属性和域间的映射关系

  F：属性间的依赖关系

  // 示例
  Students(U,D,dom,F)
  U{sno,sname,sage}　　//理解为表的字段集合(学号、姓名、年龄)
  D{char,int}　　// 理解为表中字段的类型集合
  dom{dom(sno)=dom(sname)=char,dom(sage)=int}　　// 理解为每个字段具体的取值
  F{sno-->sname,sno-->sage}　　// 理解为表字段间关系

• R(U)

  // 示例
  Students(sno,sname,sage)

• R(A/D)

  // 示例
  Students(sno:char,sname:char,sage:int)

关系实例 (Relation Instance)

一个给定关系中某一时刻的元组的集合。

实体 (Entity)

现实世界拥有独特的特性，又与其他实体有联系的对象

联系 (Relationship)

实体之间的对应关系

• 一对一联系 (1:1)
• 一对多联系 (1:n)
• 多对多联系 (m:n)

属性 (Attribute)

关系的列，描述实体的特性。

元组 (Tuple)

关系中除属性名所在行以外的其他行，每个元组均有一个分量 (component)对应关系的每个属性。

域 (Domain)

属性的取值范围。由于元组的每个分量/属性的每个值需要满足原子性，域必须属于基本数据类型。

目/度 (Degree)

关系中域的个数 $n$。

当$n=1$时，称该关系为单元关 系或一元关系。
当$n=2$时，称该关系为二元关系。
当$n=m $时，称该关系为m 元关系。

键

// 以下面关系模式为例
Students(sno,id,sname,sage,tno)
Teachers(tno,tname)

超键(super key)

在关系中能唯一标识元组的属性集称为关系模式的超键。

R1(sno,sname), R2(id,sname,sage)... // 含有sno,id可唯一标识学生的属性的任意集合都是超键

候选键(candidate key)

不含有多余属性的超键称为候选键。候选键可以是单列键，也可以是复合键。

R1(sno), R2(id) // sno和id都是Students的候选键

主键(primary key)

用户选作元组唯一标识的一个候选键。

R1(sno)
R2(id) // 可选取sno或id任一候选键为主键

外键(foreign key)

关系模式R1中不是R1的主键，而是另一个关系模式R2主键的属性，是关系模式R1的外键。

// tno是Teachers的主键, Students的外键

4. 关系代数

关系代数是过程性关系查询，任意关系运算(operations)的结果是一个关系。

• 集合运算：并、交、差

• 删除运算：投影、选择

• 二元运算：笛卡尔积、条件连接(condition join)、等值连接、自然连接、外连接、外并、除

• 五个基本运算：并(union)、差(set difference)、投影(project)、选择(select)、笛卡尔积(Cartesian product/cross-product)

  其余运算都可由这五种运算符和得到。

集合运算

具有相同关系模式的关系可以进行集合运算，以下图为例：

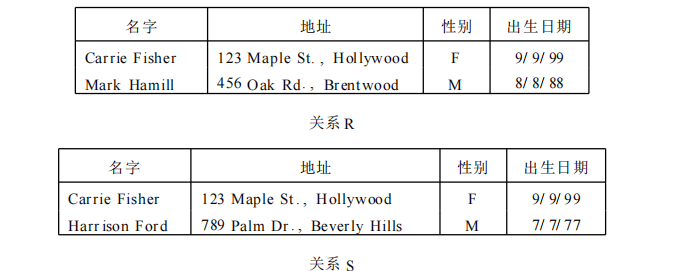
并运算，$R \cup S = \{t|t\in R\vee t \in S\}$，属于R或S的元组的集合组成的关系(R/S重复元组只出现一次)。

交运算，$R \cap S = \{t|t\in R\land t \in S\}$，属于R且S的元组的集合组成的关系。

差运算，$R - S = \{t|t\in R- t \in S\}$，属于R不属于S的元组的集合组成的关系。

投影

从关系R中产生只有R部分 列 的新关系。即从$A_1, A_2, ..., A_n$ 中得到 $\pi_a(R)$，$a \subseteq {A_1, A_2, ..., A_n}$。

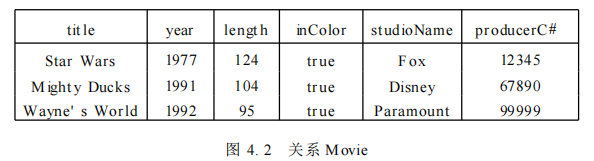
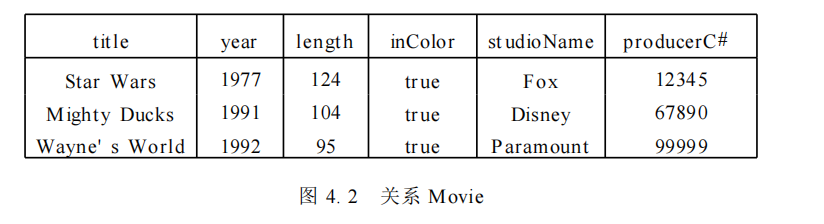
如有关系如图：

将此关系投影到前三个属性上有：

将此关系投影到单个属性inColor上得到单列关系 (消除重复元组)：

选择

从关系 $R$ 中产生只有 $R$ 部分 元组 的新关系。记为 $\sigma (R)$。

仍以此关系为例：

则对指定属性的值用表达式筛选可表示为：

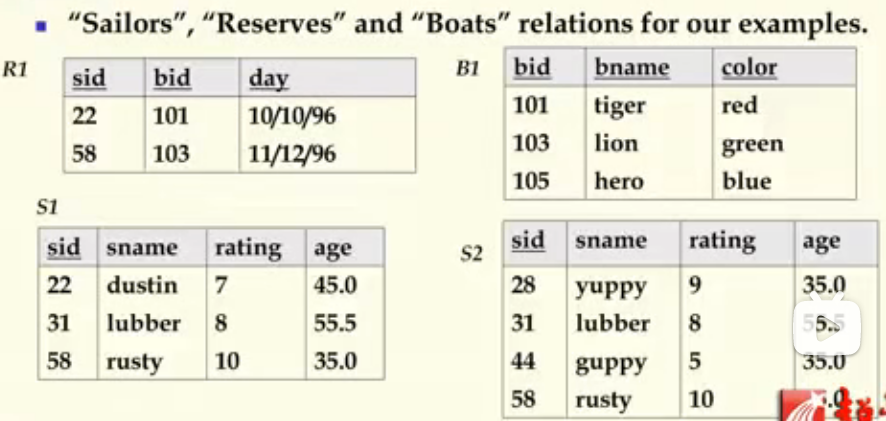
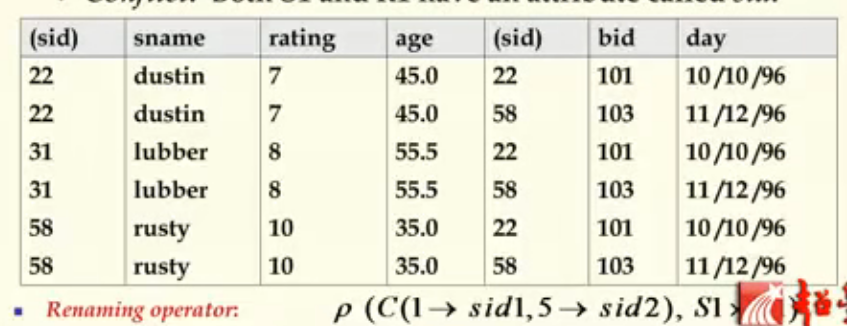
笛卡尔积

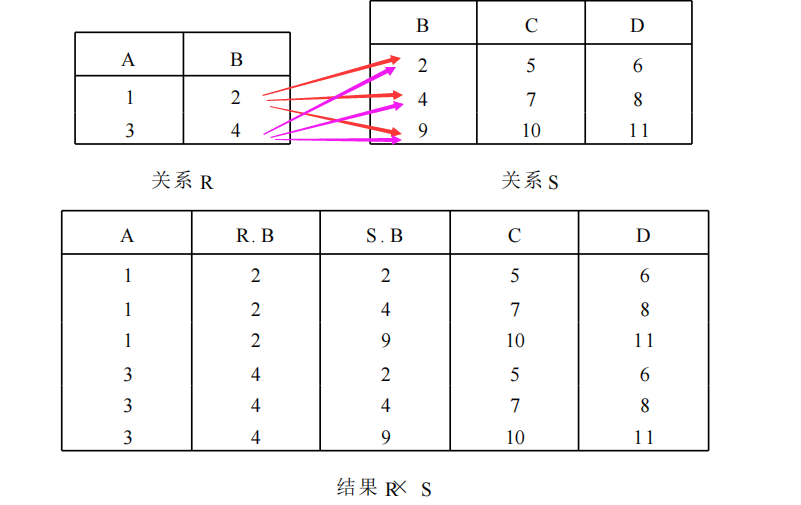
也为交叉连接，得到关系 $R$ 和关系 $S$ 逐个元组对拼接后的新关系。记为$R×S$。

$R×S$ 依次选取R中的元素对为第一元素，以 $S$ 中每个元素对为第二元素获得新关系。R和S的重名属性需要更名：

自然连接

自然连接 (natural join)，内连接中等值连接的特殊情况。即在所有重名属性上都进行等值连接，记作 ⋈，下面的等值连接亦为自然连接，对于笛卡尔积中的例子有：

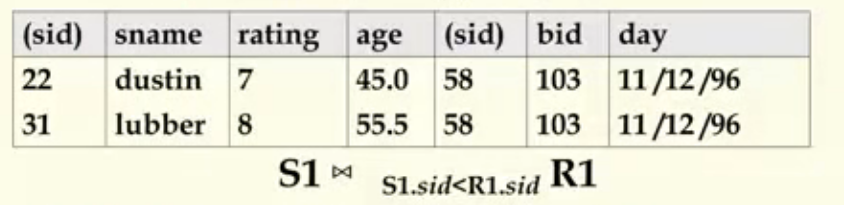
条件连接/θ连接

内连接中的不等值连接，对笛卡尔积的连接结果进行选择。

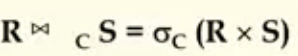
以图示关系为例：

笛卡尔积：

条件连接：

选择条件式用“ $=$ ”判断为等值连接(equi-join)：

外连接

• 左连接 (left join) *⋈：在 自然连接 的基础上加上 左关系 不包含于自然连接的元组，缺失属性填充空值。
• 右连接 (right join) ⋈*：在 自然连接 的基础上加上 右关系 不包含于自然连接的元组，缺失属性填充空值。
• 全连接(outer join) *⋈*：左连接 + 右连接

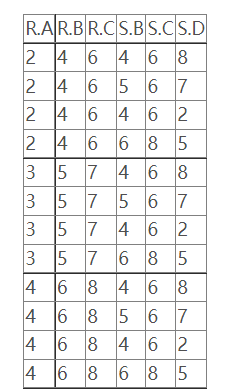
下图为例：

笛卡尔积：

自然连接：

左连接：

右连接：

全连接：

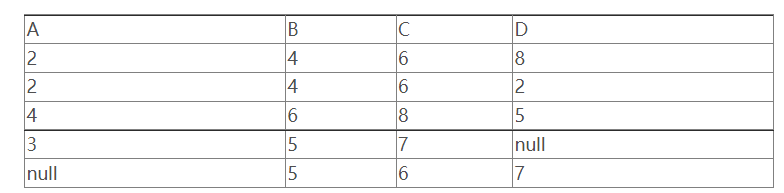
外并

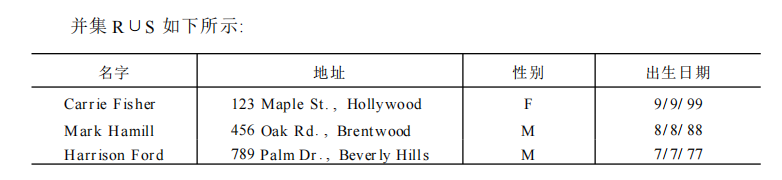
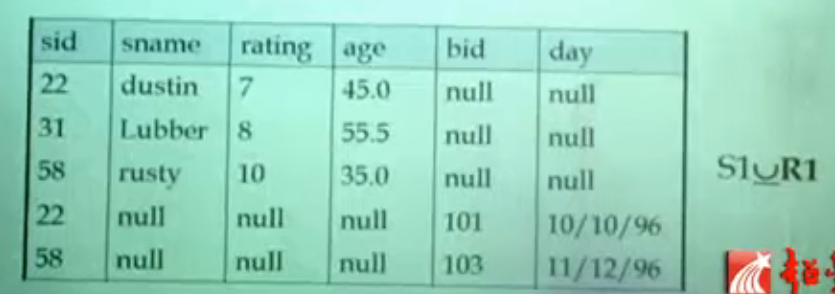
对于不同模式的关系，缺失属性填充空值的并运算。

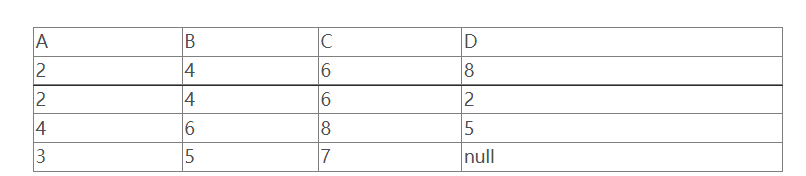
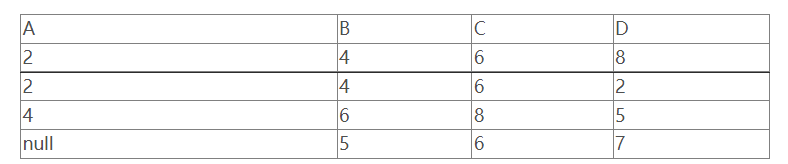
下图为例：

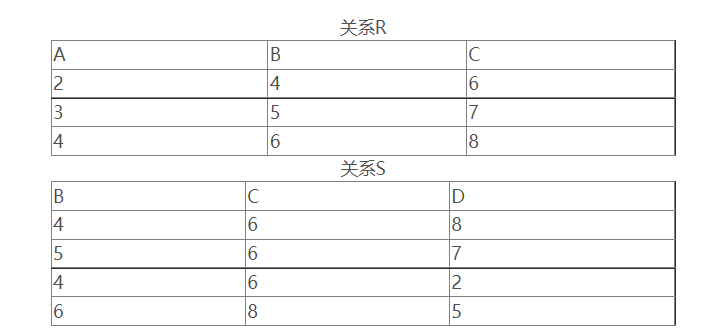
除

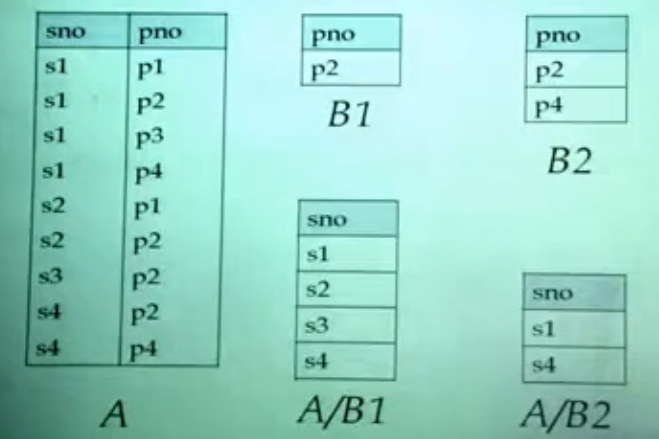
R÷S，R中非共有属性投影满足S中共有属性投影的选择。

若有R(X,Y)，S(Y,Z)：

如下例：

因此，$R(X,Y)，S(Y,Z)$时 $R/S$ 也可以写作：

$R/S = \pi_X(R) - \pi_X((\pi_X(R) \times \pi_X(R)) - \pi_{X,Y}(R))$

*综合案例

1. 求红色并且重量不超过 $15$ 的零件号和零件名

​

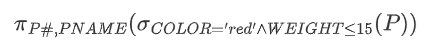
2. 求提供所有零件的供应商名称

​

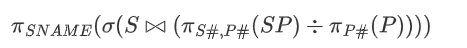
3. 求所有提供红色零件的供应商名称

   

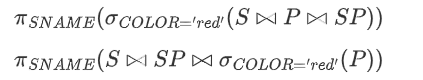
4. 求提供 $P1$ 但是不提供 $P2 $的供应商名称

   

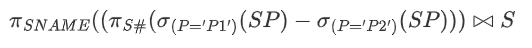
5. 关系演算

关系演算 (Rrlation Calculus)是基于逻辑而非代数的非过程性关系查询，使用谓词演算。分为元组关系演算 (Tuple Relational Calculus, TRC)和域关系演算 (Domain Relational Calculus, DRC)。

元组关系演算

以元组为单位定义变量 (variables)，得到使公式 (formula)为真的元组的集合，表达式如下：

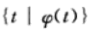
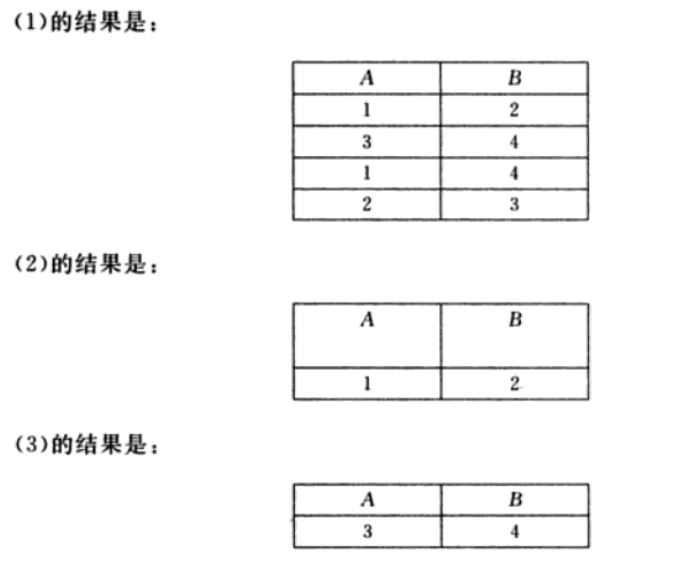
举例：

域关系演算

以属性为单位定义变量 (variables)，与元组关系演算类似：

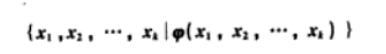
举例：

6. E-R图

参考文献

• 《数据库系统基础教程》[ 美] Jeffrey D. U llman, Jennifer Widom

• 《数据库原理及应用》 东南大学 徐立臻

• 数据库原理及应用-数据模型之层次与网状模型

• 关系模型详解【数据库概论】

• 关系模型介绍

• 外连接运算