本文最后更新于:2023年2月28日 下午
相关概念
| 术语 |
释义 |
推导 |
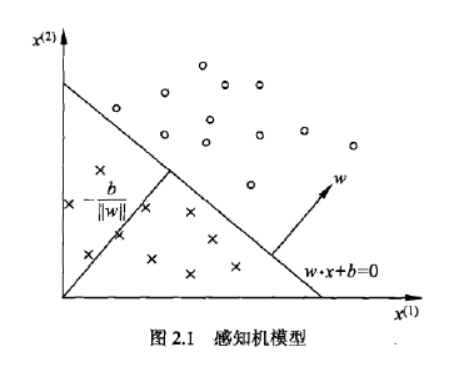
| 超平面 |
n维空间中的n-1维的子空间,即平面中的直线、空间中的平面之推广 |
w⋅x+b=0
(w,b) |
| 点到超平面的距离 |
$d = \frac{ |
\vec w \cdot \vec {x_0} + b |
| 线性可分性 |
给定一个数据集:
T={(x1,y1),(x2,y2),...,(xn,yn)},其中$ x_i \subseteq \mathbb R^n,\gamma = \lbrace+1,-1\rbrace$, i=1,2,...,n
如果存在某个超平面 w⋅x+b=0 能将数据集中的正实例点和负实例点完全正确地划分到超平面两侧,
即对所有yi=+1的正实例i,有$$\vec w \cdot \vec x + b > 0$$;
对所有yi=−1的正实例i,有$$\vec w \cdot \vec x + b < 0$$。
则称数据集T线性可分;否则,数据集T线性不可分。 |
|
原理
感知机是一个线性分类器,只适用于线性可分问题。
感知机通过训练集数据最小化损失函数的学习,得到能够将正实例点和负实例点完全分离的分离超平面 (确定w,b)。
结构
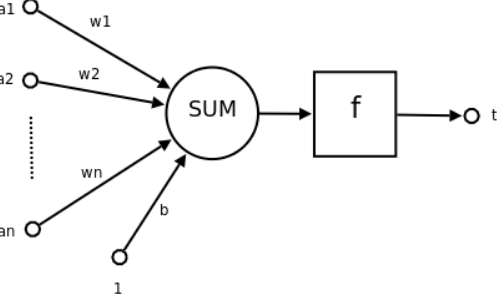
输入空间:$ x \subseteq \mathbb R^n,输入n$维特征向量
输出空间:yi∈γ,γ={+1,−1},实现二分类
感知机:∑i=1nwixi+b,w1,...,wn为各维输入分量连接到感知机的权重,b为偏置
激活函数:将结果映射至输出空间
| 函数 |
表达式 |
图像 |
| 符号函数:sign(x) |
f(x)=⎩⎪⎨⎪⎧1,x>00,x=0−1,x<0 |
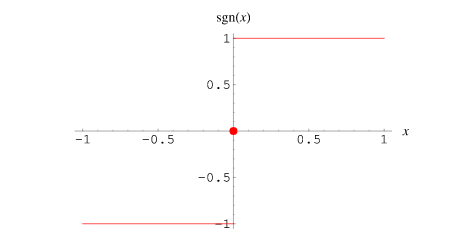 |
学习策略
损失函数
损失函数的自然选择
-
误分类点的总数。
这样的损失函数不是参数w,b 的连续可导函数,不易优化。
-
误分类点到超平面的总距离
感知机采用的损失函数
由于误分类的数据满足 (异号):
−yi(w⋅xi+b)≥0
因此,误分类点(xi,yi)到超平面的距离是:
d=∥w∥−yi(w⋅xi+b)
误分类点集合M中的点到超平面的总距离是:
d=∥w∥−∑xi∈Myi(w⋅xi+b)
忽略∥w∥1,得到感知机学习的损失函数:
L(w,b)=−xi∈M∑yi(w⋅xi+b)
学习算法
采用随机梯度下降算法 (stochastic gradient descent,SGD),解决最小化损失函数的优化问题。
目标:
minL(w,b)=−xi∈M∑yi(w⋅xi+b)
损失函数L(w,b)的梯度为:
∇wL(w,b)=−xi∈M∑yixi
\nabla_w L(w,b) = -\sum_{x_i \in M}y_i\
误分类点(xi,yi)更新w,b:
w←w+α⋅∇wL(w,b)=w+αyixi
b←b+α⋅∇bL(w,b)=b+αyi
学习算法的原始形式
-
选取初值w0,b0,α
-
选取训练集中点(xi,yi)
-
将数据输入感知机,若激活函数得到的结果yi(w⋅xi+b)≤0,则为误分类点,更新w,b
w←w+αyixi
b←b+αyi
-
转至2. ,直到训练集中无误分类点
示例:
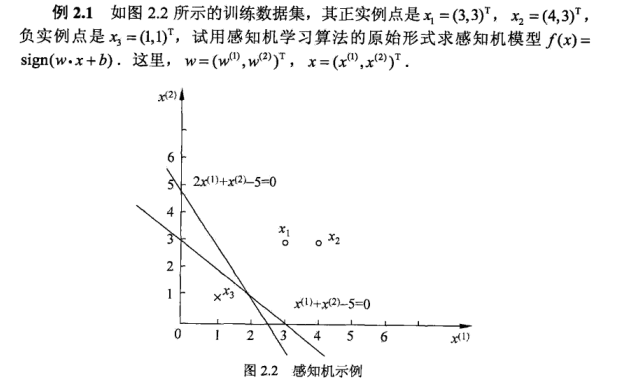
即对于x1(3,3)T,x2(4,3)T,y=1;x3(1,1)T,y=−1。
-
选取初值w0=b0=0,α=1
-
对于x1(3,3)T,得到sign(0)=0,为误分类点
-
更新w,b,w1=w0+αy1x1=(3,3)T;b1=b0+αy1=1
-
选取x1,x2均被更新后的感知机正确分类,对于x3(1,1)T,得到sign(7)=1,为误分类点
-
更新w,b,w2=w1+αy3x3=(2,2)T;b2=b1+αy3=0
-
以此类推,计算结果如下表:
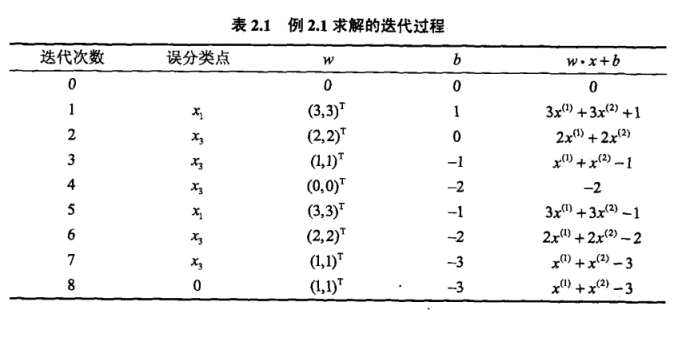
参考资料
- 《统计学习方法》- 李航
- 《机器学习》 - 周志华




