数据挖掘(一) 数据描述与分析
本文最后更新于:2023年2月28日 下午
1. 数据的概括性度量
相关概念
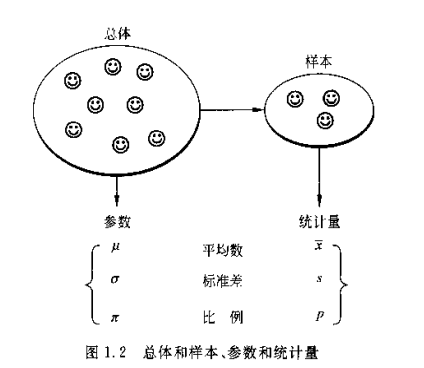
总体:包括所研究全部个体数据的集合
样本:总体中抽取的部分个体集合
样本量:样本个体数
参数:用来描述总体特征的概括性数字度量
统计量:用来描述样本特征的概括性数字度量
数据类型:分类数据、顺序数据、数值数据
分类数据是对事物的一种分类,落在某一类的数据个数为频数 (frequency)。
集中趋势
数据分布的集中趋势,反映数据向中心值聚集的倾向。
1 | |
离散程度
数据分布的离散程度,反映各变量远离中心值的程度。
对于不同类型的数据,离散程度的度量值主要为
- 分类数据:异众比率
- 顺序数据:四分位差
- 数值数据:方差、标准差
- 不同样本/总体间:离散系数
-
异众比率 (variation ratio):非众数组的频率数占总频数的比率
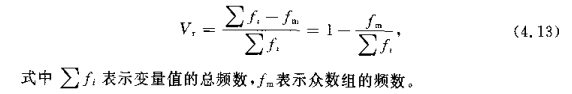
异众比率大说明众数的代表性差。
-
四分位差/内距/四分间距 (quartile deviation):上四分位数与下四分位数的差
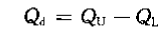
反映中间50%数据的离散程度,说明中位数的代表性。
数值越小,中间数据越集中,中位数代表性好。
-
极差 (range):最大值与最小值之差
-
平均差/平均离差 (mean deviation):各变量值与其平均数离差绝对值的和的平均数
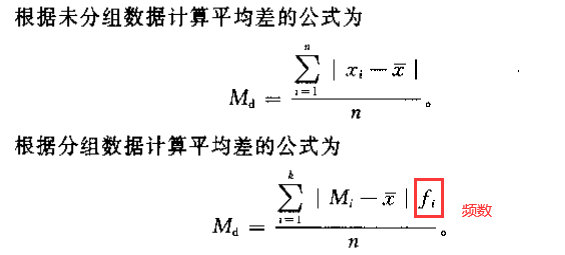
-
方差 (variance):通过绝对值消去离差正负号,为各变量值与其平均数离差平方的和的平均数(用自由度计算平均数)
自由度 (degree of freedom):计算某一统计量时,取值不受限制的变量个数。如在计算方差时,限制条件是样品平均数,因此可自由取值的变量数为。
自由度的计算: (自由度,样本个数,约束条件个数)
自由度是在用样本统计量推断总体参数时,为支持“统计量与总体参数相等”的理论假设提出的。 通常表示实际需要计算的参数的数量。例如,一组数据,平均数一定,则这组数据有个数据可以自由变化;如一组数据平均数一定,标准差也一定,则有个数据可以自由变化。
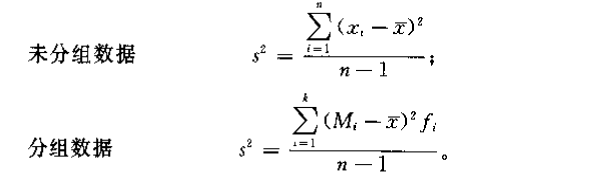
-
标准差 (standard deviation):方差的平方根。具有量纲,与变量值的计量单位相同。
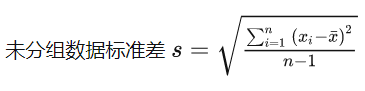
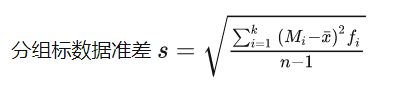
-
标准分数/分数 (standard score):变量值与平均数的离差除以标准差可得到每个变量的标准分数,反映变量在该组数据中的相对位置。
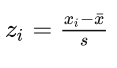
如某数的标准分数为,则该数低于均值倍的标准差。
标准分数的公式同样可以用作数据标准化,消除量纲影响。它使数据的均值为 ,标准差为 ,并未改变数据分布的形状。
-
离散系数/变异系数 (coefficient of variation):标准差与均值之比,用于比较平均水平或量纲不同的不同组别数据的离散程度。
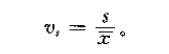
离散系数越大,离散程度越大。
-
离群点/异常值 (outlier) 判断方法
-
经验法则
对于对称分布的数据,

因此,在平均数个标准差外的数值为离群点。
-
切比雪夫不等式 (Chebyshev’ s inequality)
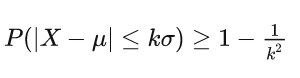
k>0,μ 是均值, σ 是标准差。上式意为至少有的概率变量数值落在均值个标准差的范围内。
如时:

-
分布形状
数据分布的形状,反映数据偏斜程度、分布扁平程度、是否对称等。
-
偏态 (skewness):数据分布的不对称性
利用中位数、平均数、众数间关系大体判断偏态:
众数,中位数,平均数,
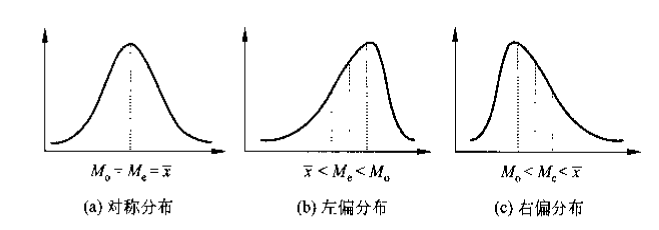
-
偏态系数:对数据分布不对称性的度量值,记作
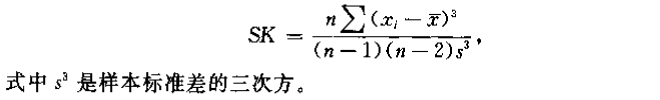
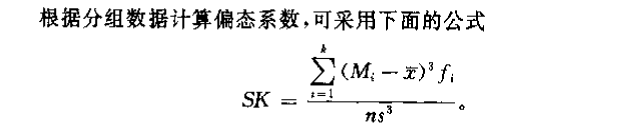
偏态系数为,分布是对称的(离差三次方的正负离差抵消);偏态系数为正,分布右偏;偏态系数为负,分布左偏。
偏态系数越大,偏斜程度越大。
-
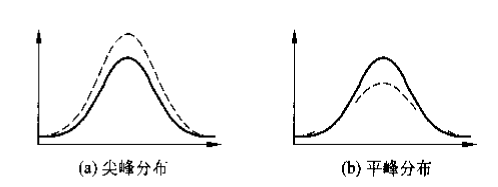
峰态 (kurtosis):数据分布的平峰或尖峰程度
-
峰态系数:对数据分布峰态的度量值,记作
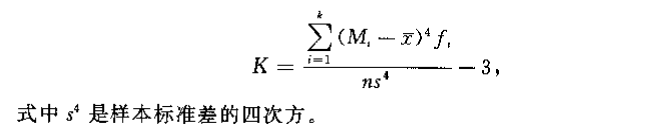
峰态系数为,为标准正态分布;峰态系数为正,尖峰分布;峰态系数为负,平峰分布。
2. 基本图表
直方图/折线图/饼图
表示分类数据的频数分布。
累积频数图/累计频率图
累积频数 (cumulative frequencies):将顺序数据的频数按一定方向逐级累加。
从顺序数据开始处向后累加为向上累积;
从顺序数据结束处向前累加为向下累积;
环形图
相对饼图表示单个样本或总体的频数分布,环形图可以表示多个样本或总体。
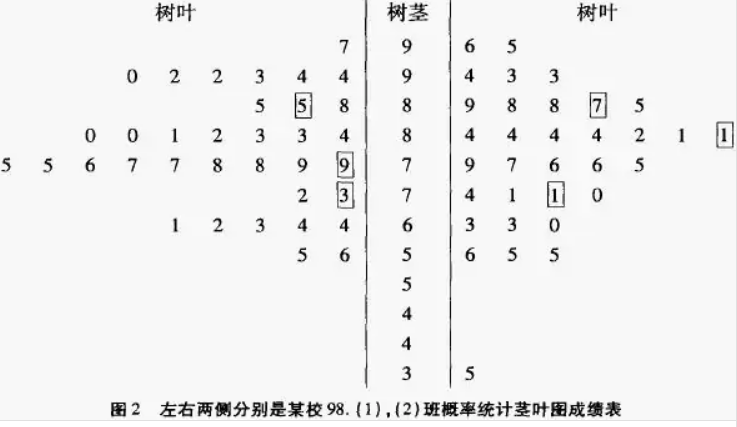
茎叶图
由数值组成,以指定位数数值为“茎”,指定位数数值为“叶”,可以反映数据的离散程度和分布形状。
箱线图
箱线图 (box plot):由一组数据的最大值、最小值、中位数、两个四分位数共五个特征组成。
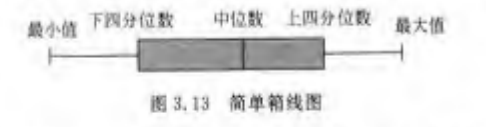
箱线图可以反映数据分布特征:
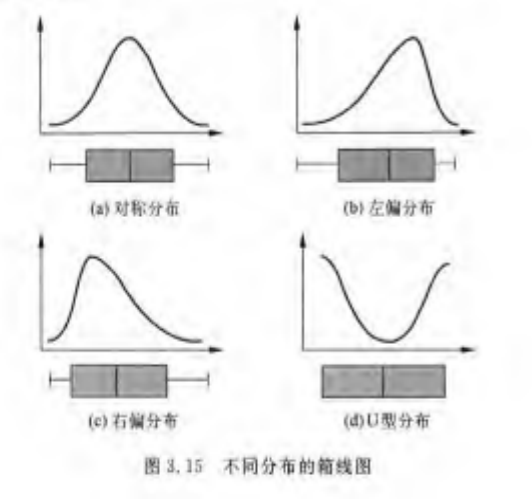
多个单批箱线图并列易于直观比较:
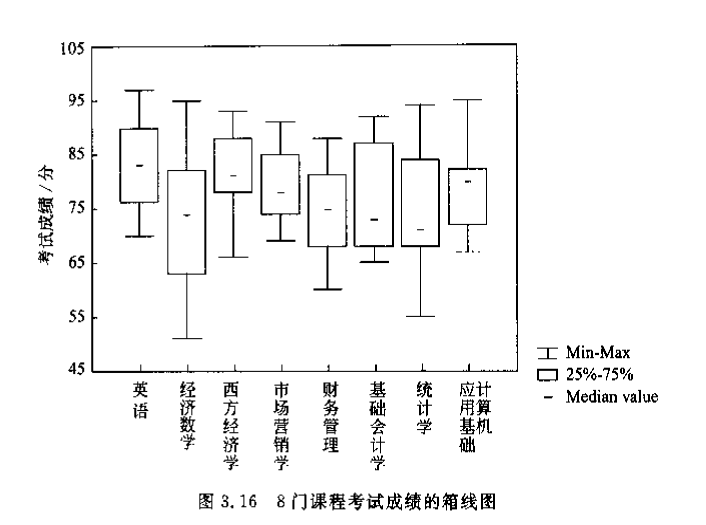
3. 聚合统计
参考资料
- 《统计学》 贾俊平
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!