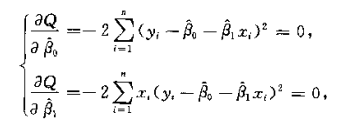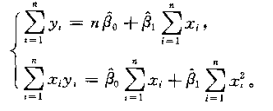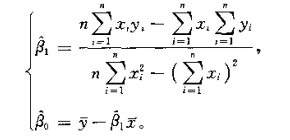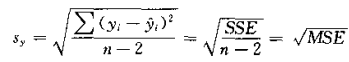统计学(五) 相关与回归分析

方差分析是研究分类型自变量与数值型因变量之间关系的统计方法

相关（度量变量之间的关系强度）与回归（探究变量之间的数据伴随关系）分析是研究数值型变量之间关系的统计方法

• 两个变量：简单相关与简单回归分析
• 多个变量：多元相关与多元回归分析

1. 变量间关系

按关系形态，变量间关系可分为：

1. 函数关系：因变量完全依赖于自变量
2. 相关关系：变量之前存在不确定数量关系

相关关系的度量

相关系数 (correlation coefficient)

根据样本数据计算的对两个变量之间线性关系强度的度量值.总体相关系数记为 $\rho$，样本相关系数记为 $r$。

2. 一元线性回归

一元线性回归模型

模型建立

因变量 (dependent variable)

回归分析中，被预测或被解释的变量，记为 $y$

自变量 (independent variable)

回归分析中，用来预测或解释的一个或多个变量，记为 $x$

回归模型 (regression model)

描述因变量 $y$ 如何依赖于自变量 $x$ 和误差项 $\epsilon$ 的方程

如一元线性回归模型：

$y = \beta_0+\beta_1 x + \epsilon$

• $\beta_0+\beta_1 x$ ：反映由 $x$ 变化引起的 $y$ 的线性变化，$\beta_0,\beta_1$ 是模型的参数（常数）

• $\epsilon$ ：误差项的随机变量，反映除$x$ 变化引起的 $y$ 的线性变化之外随机因素对 $y$ 的影响，满足 $\epsilon \sim N(0,\sigma^2)$

回归方程 (regression equation)

描述因变量 $y$ 的期望值如何依赖于自变量 $x$ 的方程

如一元线性回归方程（直线回归方程）：

$E(y)=\beta_0+\beta_1 x$

估计的回归方程 (estimated regression equation)

利用最小二乘法，根据样本数据求出回归方程的估计

如一元线性的估计的回归方程：

$\hat {y} = \hat{\beta_0}+\hat{\beta_1}x$

• $\hat{\beta_0}$：回归直线在 $y$ 轴上的截距的估计
• $\hat{\beta_1}$：回归直线斜率的估计
• $\hat y$：$y$ 的估计

参数的最小二乘估计 (method of least squares)

最小二乘法是使因变量的观测值 $y_i$ 与估计值 $\hat{y_i}$ 之间的离差平均和最小求得 $\hat{\beta_0},\hat{\beta_1}$

最小二乘法的目标函数：

$min \sum(y_i-\hat{y_i})^2=min \sum(y_i-\hat{\beta_0}-\hat{\beta_1}x_i)^2$

根据极值定理可得关于参数 $\beta_0,\beta_1$ 偏导数的等式:

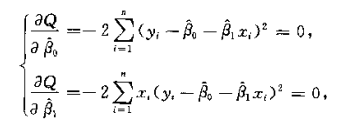
化简得到参数 $\beta_0,\beta_1$的标准方程组：

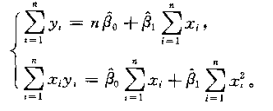
解标准方程组得到参数 $\beta_0,\beta_1$的表达式：

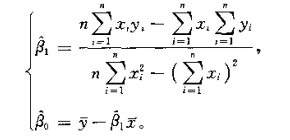
模型评估

回归直线对数据的拟合优度 (goodness of fit)

回归直线与各观测点的接近程度，通过判定系数度量

判定系数 (coefficient of determination)

回归平方和占总平方和的比例，记为 $R^2$

总平方和、回归平方和、残差平方和

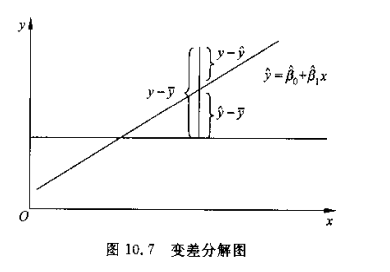
• 反映因变量 $y$ 取值的波动（变差）：观测值 $y_i$ 与均值 $\overline y$ 的离差平方和，总平方和 $SST$

  $SST=\sum(y_i-\overline y)^2$

• 反映自变量 $x$ 与因变量 $y$ 之间的线性关系造成的波动：预测值 $\hat {y_i}$ 与均值 $\overline y$ 的离差平方和，回归平方和 $SSR$

  $SSR=\sum(\hat{y_i}-\overline y)^2$

• 反映线性关系外其他因素造成的波动：观测值 $y_i$ 与预测值 $\hat {y_i}$ 的离差平方和，残差平方和 $SSE$

  $SSE=\sum(y_i-\hat{y_i})^2$

• 平方和间关系

  $SST=SSR+SSE$

判定系数 $R^2$

$R^2=\frac{SSR}{SST}=\frac{\sum(\hat{y_i}-\overline y)^2}{\sum(y_i-\overline y)^2}$

可化为关于 $x_i,y_i,\overline x,\overline y,$ 的关系式

$R^2=[\frac{\sum{(x_i-\overline x)(y_i-\overline y)}}{\sqrt {\sum(x_i-\overline x)^2 \sqrt {\sum(y_i - \overline y)^2}}}]^2$

相关系数 $r$

判定系数的平方根，与回归系数 $\hat{\beta_1}$ 符号相同

$r=\frac{\sum{(x_i-\overline x)(y_i-\overline y)}}{\sqrt {\sum(x_i-\overline x)^2 \sqrt {\sum(y_i - \overline y)^2}}}$

1. $|r|$ 越接近 $1$，拟合程度越高
2. $r$ 不能直接说明拟合优度，如 $r=0.5$ 时，$R^2=0.025$，回归平方和只能解释总变差的 $25\%$，而非 $50\%$

估计量的标准差/标准误差 (standard error of estimate)

均方残差的平方根 ($MSE$)，反映了用估计的回归
方程预测因变量 $y$ 时预测误差的大小，记作 $s_y$

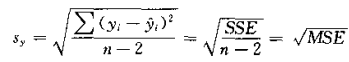
1. $s_y$ 越小，回归直线对各观测点的代表性就越好,
2. 由于估计的回归方差由最小二乘法得到，其目标就是使 $\sum(y_i-\hat{y_i})^2$ 最小，因此回归直线是估计标准误差最小的直线

显著性检验

检验模型方程是否真实反映了自变量 $x$ 和因变量 $y$ 间的关系，主要包括：

• 线性关系的检验
• 回归系数的检验

线性关系的检验

检验自变量 $x$ 和因变量 $y$ 间的线性关系是否显著，能否用线性模型表示

1. 提出假设

   

2. 计算检验统计量 $F$

   $F=\frac{MSR}{MSE}=\frac{\frac{SSR}{1}}{\frac{SSE}{n-2}} \sim F(1,n-2)$

   当线性回归的自变量个数为 $p$ 时：

   • $SSR$ 自由度为 $p$，一元线性回归中为 $1$
   • $SSE$ 自由度为 $n-p-1$，一元线性回归中为 $n-2$

3. 决策

   查 $F$ 分布表得到 $df=(1,n-2)$ 处的临界值 $F_{\alpha}$

   • $F>F_{\alpha}$，拒绝 $H_0$
   • $F<F_{\alpha}$，不拒绝 $H_0$

模型预测