R与数据分析(一) 回归模型
本文最后更新于:2023年2月28日 下午
1. 模型的建立
1.1 线性模型(the linear model)
原理
回归方程 (regression equation), the expected value of given :
估计的回归方程 (estimated regression equation), the estimated value of :
回归模型 (regression model)
the exact value of :
the estimated value of :
(error) : 误差项的随机变量,反映除 变化引起的 的线性变化之外随机因素对 的影响,满足
- : independent —— 样本相互独立 (every observation to be independent of every other observation)
- : identically distributed —— 方差齐性 (the equality of variance assumption, (EOV))
- : distribute_d normally —— 误差项正态分布 ( must be from a normal distribution, at least approximately)
最小二乘法(least squares)
Residual (残差):
1 | |
Residual Sum of Suqares (残差平方和)
1 | |
Residual Standard Error (残差标准差)
实现
1 | |
1 | |
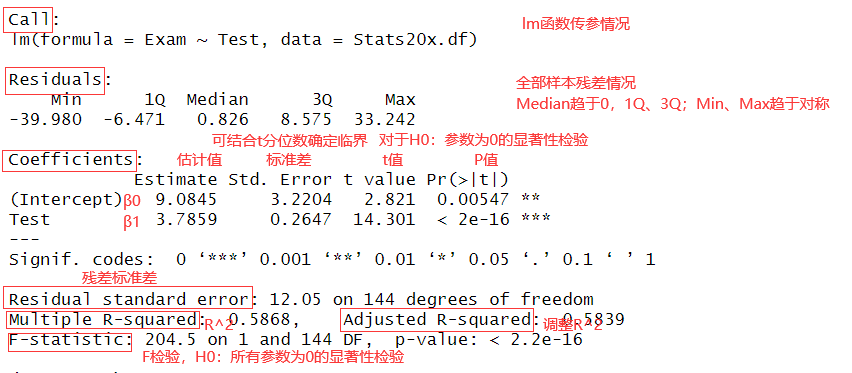
1 | |
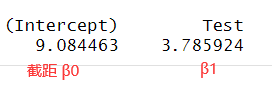
1 | |

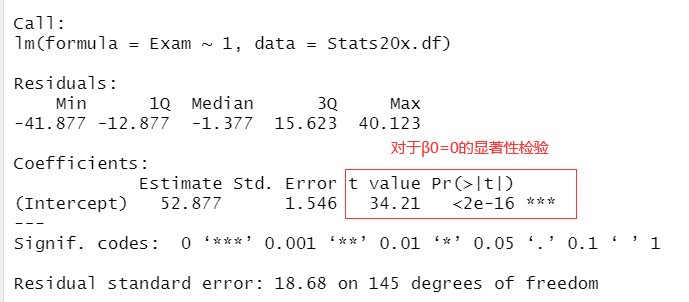
1.3 零模型(the null model)
原理
假设自变量与因变量之间没有关系的模型为零模型。
: Test 和 Exam 间没有关系
零模型残差:
Total Sum of Squares (零模型残差平方和)
Multiple R-squared
We can say that $ R^2 \times 100% $ of the variation in the exammark is explained by using a straight line relationship (i.e., simple linear
model) with test score.
说明拟合效果越好
Explained Sum of Squares (回归平方和)
Adjusted R-squared 调整
实现
1 | |

1.4 t检验(t-test)
单样本t检验(one-sample t-test)
单样本 检验用于比较样本均值与一个特定数值之间的差异情况。前提条件为样本数据的因变量满足正态分布。
检验的计算公式
值可由样本均值 $ \overline y$、标准差 、样本个数 得到,满足自由度为 的 分布:
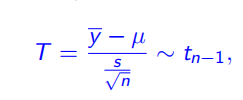
临界值 (t-multiplier) 取决于自由度和置信水平。置信水平为 (双尾) 时有:

置信区间可以表示为:
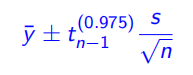
1 | |
-
-
lm(Exam~1)零模型summary(null.fit)得到 的 值,值越小越拒绝confint(null.fit)得到 置信水平为 的置信区间 -
t.test(Stats20x.df$Exam,mu=0)
-
-
-
t.test(Stats20x.df$Exam,mu=60)
-
nullmu.fit=lm(I(Exam-60)~1,data=Stats20x.df)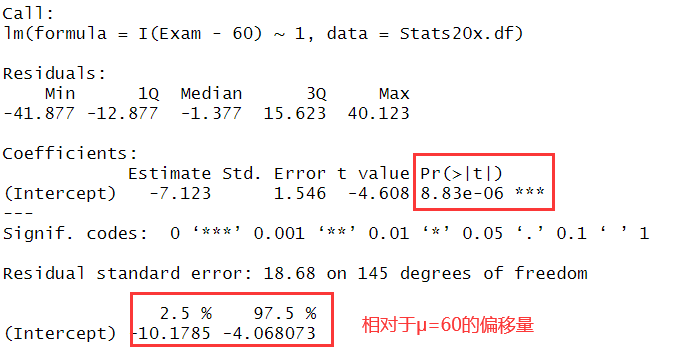
-
配对t检验(the paired t-test)
配对 检验用于分析配对定量数据之间的差异对比关系。前提条件为配对数据的差值满足正态分布。配对数据是指相互连接或关联 (不相互独立),样本量相同的数据。
The paired t-test is just an application of the one-sample t-test applied to differences.
以本例中的 Exam 和 Test 为例,检验 if the midterm test marks and exam marks have the same expected value.
1 | |
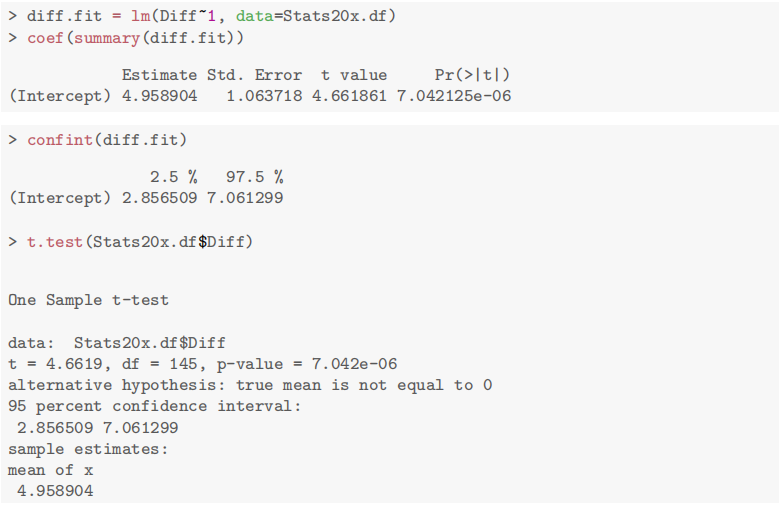
由图可知
- P-value
- this difference to be about 2.9 to 7.1 marks
1.5 广义线性模型(generalized linear mode)
二次模型(quadratic model)
The quadratic model:
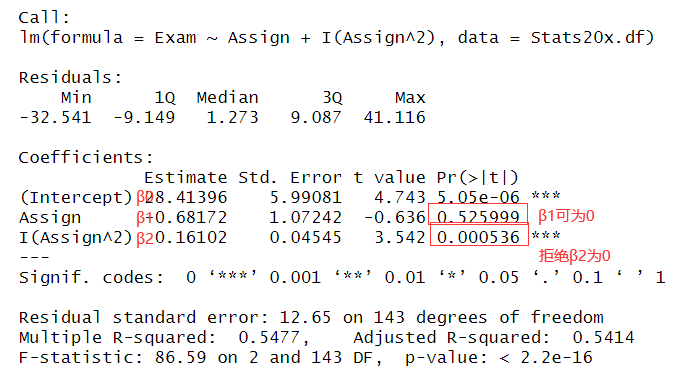
以 Exam 和 Assign 为例
1 | |
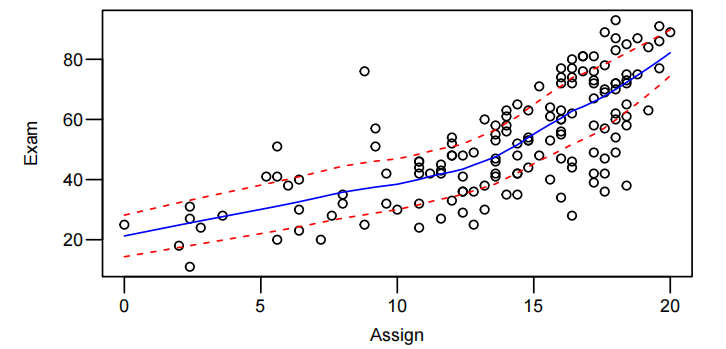
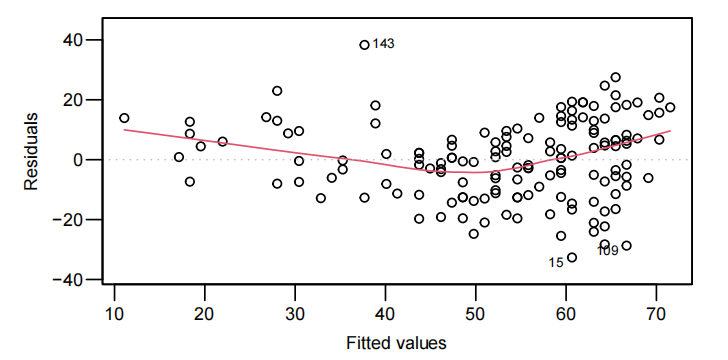
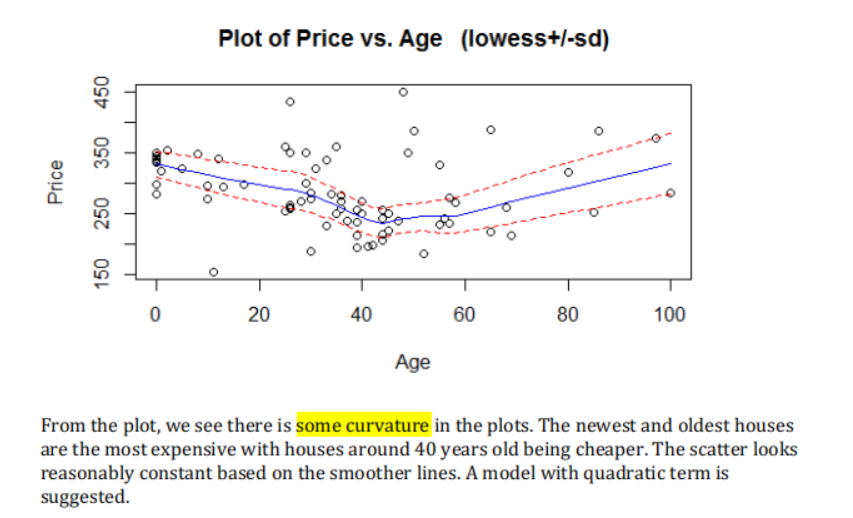
从两图中能得到结论:Sure looks like some curvature, but, at least the scatter looks fairly constant around this curve.
1 | |
二分类模型 (2-level categorical variable model)
哑变量 (Dummy Variable)
在构建回归模型时,
- 如果自变量 为连续性变量,回归系数 (slope) 可以解释为:在其他自变量不变的条件下, 每改变一个单位,所引起的因变量的平均变化量;
- 如果自变量为二分类变量,例如是否饮酒(1=是,0=否),则回归系数 (slope)可以解释为:其他自变量不变的条件下,(饮酒者)与 (不饮酒者)相比,所引起的因变量 的平均变化量。
当自变量 为多分类变量时,引入哑变量(Dummy Variable),又称为虚拟变量将各个多分类变量均转化为0-1变量。
以 Exam 和 Attend 为例
The 2-level categorical variable model:
- is the mean exam mark for non-attenders
- is the mean mark for attenders
so β1 is the difference in mean mark for attenders compared to non-attenders.
To test the null hypothesis of no attendance effect, .
1 | |
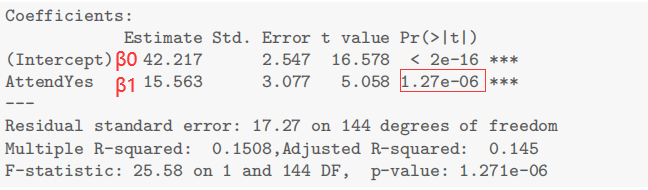
, We have extremely strong evidence that attendance is related to exam score.
1 | |
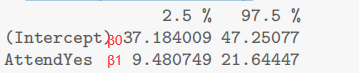
Regular attenders will obtain an increased exam mark of between 9.5 to 21.6 compared to non-attenders.
The expected exam mark of a student who regularly attends class is 9.5 to 21.6 marks higher than that of a non-attendee.
乘法模型(multiplicative model)
应用乘法模型对数据拟合的三个原则
-
数据右偏分布
right skewed, median < mean
-
数据指数增长(exponential growth)或指数下降(exponentialdecay)
-
常识
This type of right-skew distribution is very common when it comes to things involving money , resources, growth, salary, age, advantage
and energy, to name but a few.
-
残差图 (residuals vs fitted values) 呈漏斗状
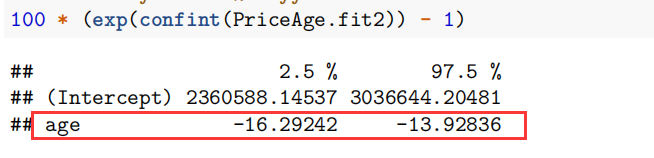
以 House Price 和 Age 为例
The multiplicative model:
-
由于数据经过对数变换后 mean 改变,median 不变。所以 视为对 median 的描述。
-
depreciation (增长率)
点估计增长率: 取得点估计值
- 时 每增加一个单位, 的 median 增加了
- 时 每增加一个单位, 的 median 减少了
区间估计增长率: 取得区间估计值
- 时 每增加一个单位, 的 median 增加了
- 时 每增加一个单位, 的 median 减少了
1 | |

1 | |

1 | |
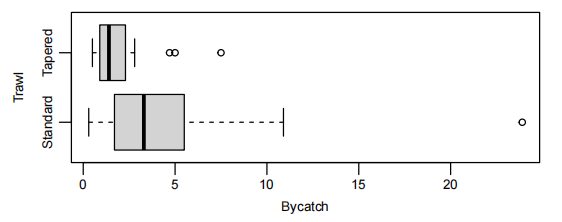
分类变量的乘法模型 (Multiplicative model with categorical explanatory variable)
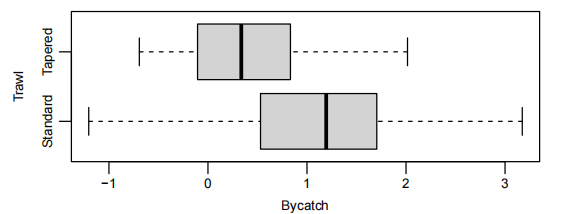
以 Bycatch 和 Trawl 为例
1 | |
1 | |
添加 后
1 | |
幂律模型 (power law model)
1.6 多元线性回归模型 ()
1.7 模型检验(checks of model assumptions)
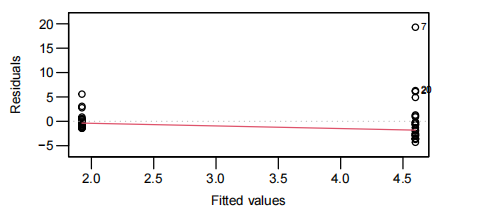
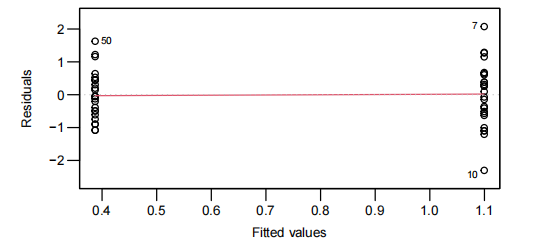
EOV check
检测线性模型是否合适。
1 | |
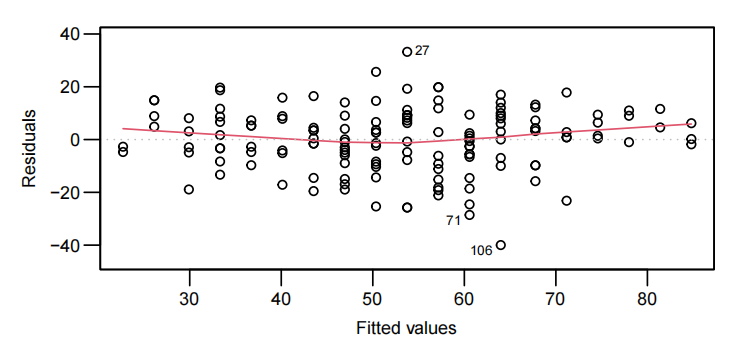
绘制 resuidual values - fitted values 散点图
由于 The residuals will be randomly scattered around 0,r-f scatter中红线期望为$ y=0$ 的水平直线。
如果红线呈曲线,则需要考虑广义线性模型中的变式。
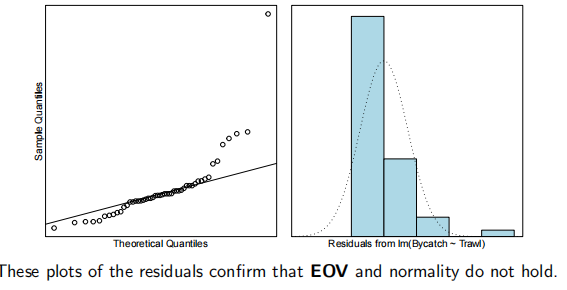
normality check
检测样本是否满足正态分布。
1 | |
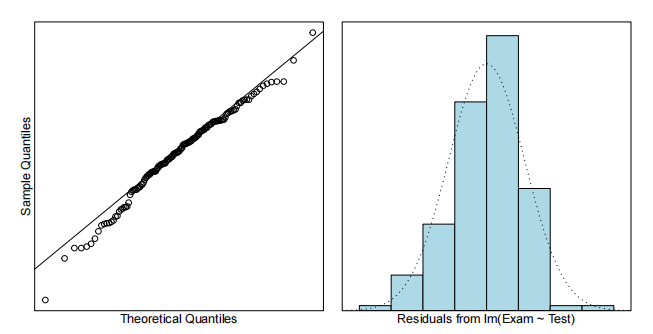
直方图
根据直方图及去实现可以判断样本是否满足正态分布以及是否 左偏 (lef skewed)、右偏 (right skewed) 等。
qq图
Q-Q图是一种散点图,横坐标为某一样本的分位数,纵坐标为另一样本的分位数。通过Q-Q图可以判断样本与模型是否大致符合以及是否存在离群点。
outlier check
检测离群点。
1 | |
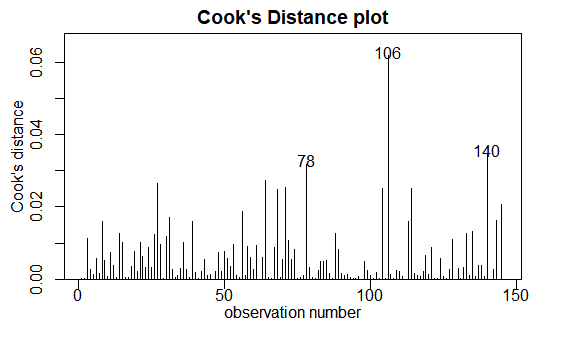
Cook距离越大,此点对模型的影响越大,异常的可能性越大。an observation is deemed to be influential if:
• Removal of the observation changes any estimated parameter value by more than one standard error, or
• Its Cook’s distance is greater than 0.4
1.8 模型预测与评估(estimation of fitted values)
模型预测
1 | |

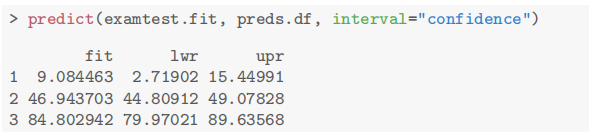
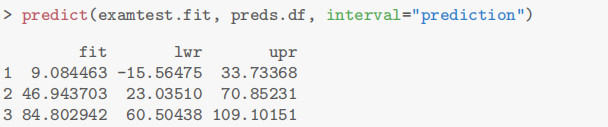
1 | |
2. 模型的实现流程
graph LR;
Question_of_interest/goal_of_the_study ---> Read_in_and_inspect_the_data ---> Fit_model ---> Model_check ---> Method_and_Assumption_Checks ---> Executive_Summary
Question_of_interest/goal_of_the_study
we are interested in a numerical response variable y (e.g.: Exam) and its relationship with a possible explanatory variable x (e.g.:Test).
Read_in_and_inspect_the_data
-
数据的读入
1
2
3
4
5
6# s20x库中有部分封装好的函数
library(s20x)
# 1. 数据读入
# header=T 首行为字段名
Stats20x.df = read.table("Data/STATS20x.txt", header=T)
-
数据的散点图描述
根据散点图描述关系种类,提出合适的模型
1
2
3
4
5
6
7
8# 2. 数据描述
# 2.1 基本统计量
# 维度
dim(Stats20x.df)
# 统计量合集
# Min,Max,Mean
# 1st Qu<-lower quartile,Med<-median,3rd Qu<-upper quartile,
summary(Stats20x.df$Exam)
1
2
3
4
5
6
7
8
9# 2.2 基本图像
# 散点图
plot(Exam~Test,data=Stats20x.df)
# library(s20x),平滑拟合函数趋势
# blue: locally weighted scatterplot smoothing smoother to the data(局部加权散点图平滑器)
# red: estimates of the variation about that line(添加固定数值的浮动变量)
trendscatter(Exam~Test, data = Stats20x.df)
# 直方图
hist(Stats20x.df$Exam,breaks=20,main="")
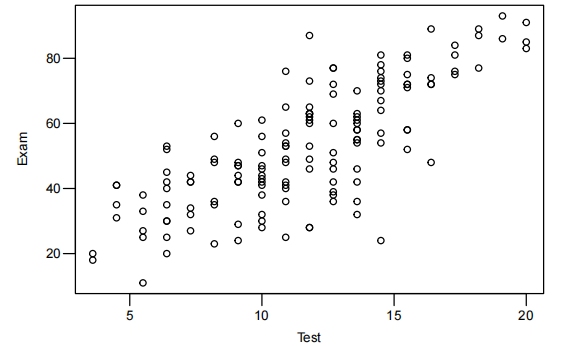
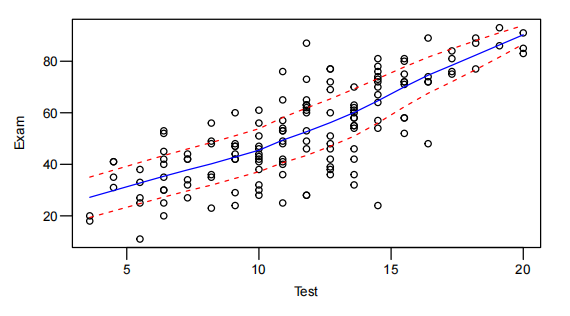
-
案例
-
简单线性模型
-
二次模型
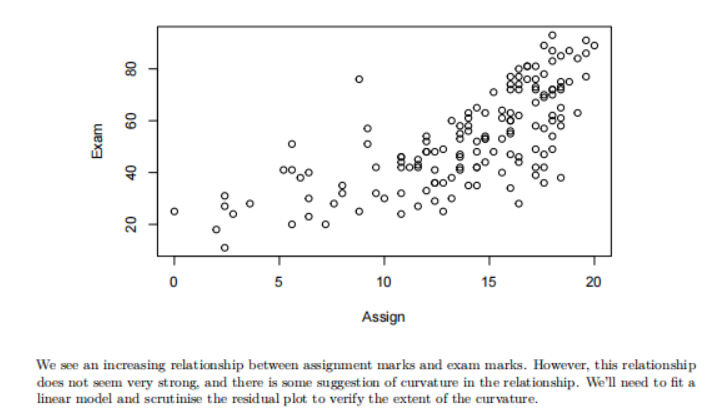
-
对数模型
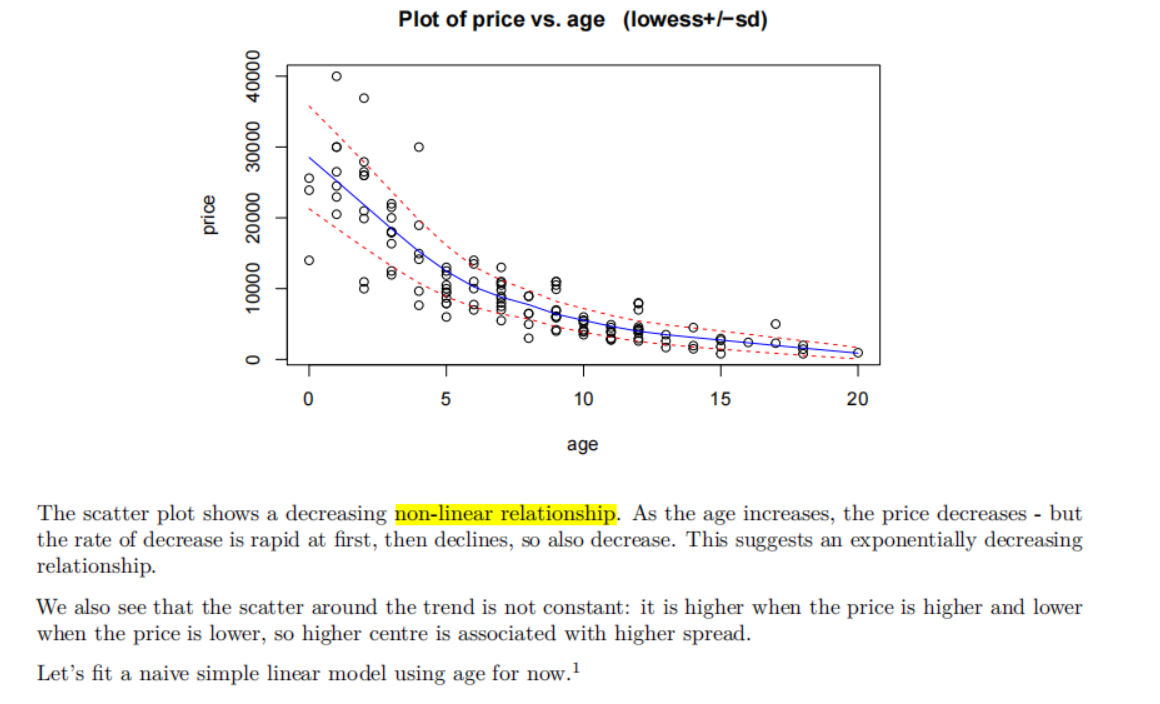
Fit_model
-
使用
lm函数实现模型 -
模型检验
-
EOV check
1
plot(examtest.fit, which = 1), -
Norm check
1
2# library(s20x)
normcheck(examtest.fit) -
Outlier check
1
2# library(s20x), 可画出每个点的Cook距离
cooks20x(examtest.fit)
-
Method_and_Assumption_Checks
-
关联关系与初步建模
案例 表述 Assignment1 - Q1 Since we have a linear relationship in the data, we have fitted a simple linear regression model to our data. Assignment1 - Q2 We have applied a one sample t-test to it, equivalent to an intercept only linear model (null model). Assignment1 - Q3 第6章案例 The scatter plot of age vs price showed clear nonlinearity and an increase in variability with price. -
模型调整
根据 Fit_model 中的代码及生成图像描述每个模型、该模型模型检验情况、模型调整方向。
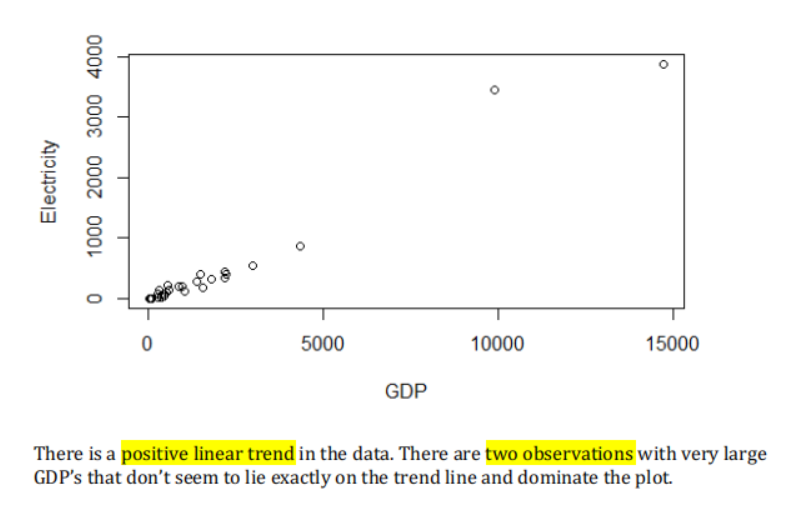
案例 表述 Assignment1 - Q1 The initial residuals and Cooks plot showed two distinct outliers USA and China). So we **limited **our countries and therefore could be following a totally different pattern so we limited our patternless scatter with fairly constant variability - so no problems.
The normaility checks don’t show any major problems (slightly long tails, if anything) and the Cook’s plot doesn’t reveal any further unduly influential points. Overall, all the model assumptions are satisfied.Assignment1 - Q2 Assignment1 - Q3 After fitting the quadratic, the residuals were fine, there were no problems with normality and no unduly influential points. We have independence from taking a random sample. 第6章案例 Residuals from a simple linear model showed failed the equality of variance and no-trend assumptions, and so the prices were log transformed. A simple linear model fifitted to logged price satisfified all assumptions. -
最终模型方程式
Our model is: <方程式>
案例 模型 表述 Assignment1 - Q1 简单线性模型 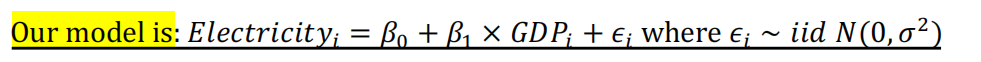
Assignment1 - Q2 零模型 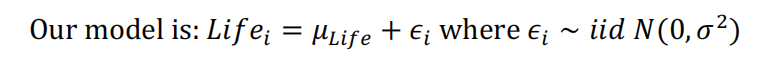
Assignment1 - Q3 二次模型 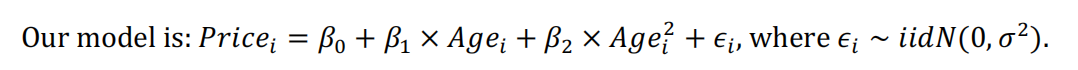
第6章案例 对数模型 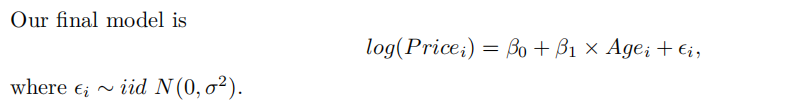
-
模型评价(以 为指标)
Our model explains of the total variation in the response variable, and so will be reasonable for prediction.
Executive_Summary
-
研究问题
Question_of_interest/goal_of_the_study
-
研究结论及依据
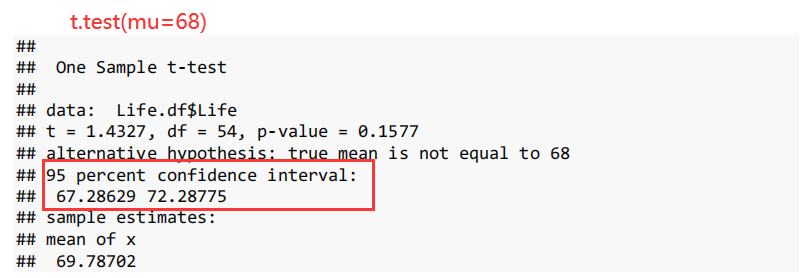
案例 模型 表述 Assignment1 - Q1 简单线性模型 We restricted our analysis to countries with GDP less than 6,000 billion dollars. Assignment1 - Q2 零模型 We estimate that the mean life expectancy is somewhere between 67.3 and 72…3 years. This is consistent with the mean life expectancy being 68 years old. [Or we do not have any evidence to suggest that the mean life expectancy is different from 68 years.) 
Assignment1 - Q3 二次模型 第6章案例 对数模型 There was clear evidence the price of the cars was exponentially decreasing as the cars got older (P-value ≈ 0) -
结论定量说
案例 模型 表述 Assignment1 - Q1 简单线性模型 We have strong evidence suggesting that electricity consumption is positively related to the GDP. Assignment1 - Q2 零模型 \ Assignment1 - Q3 二次模型 第6章案例 对数模型 We estimate that the median price for new Mazda cars (in 1991) was between A$23,600 to A$30,400 (to the nearest A$100). 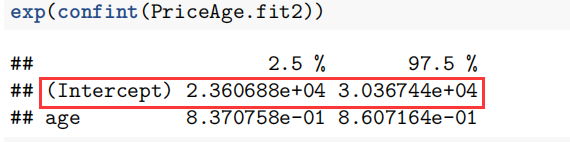
-
预测值定量说明
案例 模型 表述 Assignment1 - Q1 简单线性模型 For each additional 100 billion dollars increase in GDP, the average electricity consumption increased by somewhere between 17 and 21 billion kilowatt- hours. 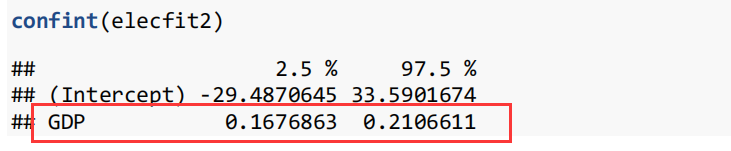
Assignment1 - Q2 零模型 \ Assignment1 - Q3 二次模型 第6章案例 对数模型 We estimate that each additional year in age results in depreciation of between 13.9% to 16.3%. 
参考资料
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!