统计学(二) 参数估计
本文最后更新于:2023年2月28日 下午
1. 三种分布
为了通过样本统计量()推断总体参数(),并判断推断的可靠性,引入抽样分布。注意,总体分布、样本分布是随机变量的频数分布;抽样分布是统计量的频数分布。
总体分布
总体分布 (population distribution):总体中各元素观察值的频数分布。
样本分布
样本分布 (sample distribution):总体中抽取的某容量为 的样本中各元素观察值的频数分布。
抽样分布
抽样分布 (sampling distribution):重复抽取容量为 的样本并计算样本某一统计量,该统计量所有可能取值的频数分布。
如在重复选取容量为 的样本时,由样本方差的所有可能取值形成的相对频数分布,称为样本方差的抽样分布。
一个例子区分三种分布:
设一个总体共有 个元素,元素的取值分别为: 。从总体中采取重复抽样方法抽取容量为 的随机样本,写出样本均值 的抽样分布。
-
总体分布
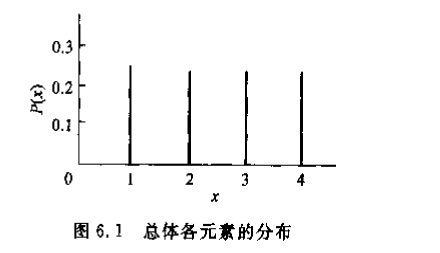
-
样本分布(共 个容量为 的样本)
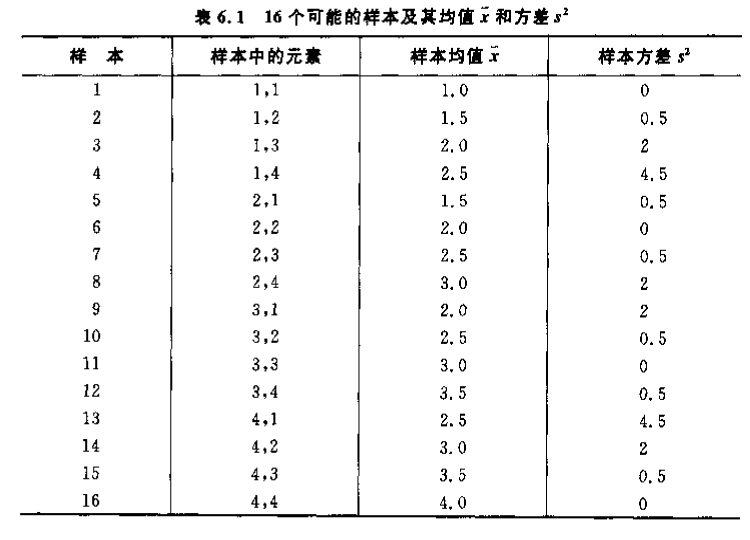
-
抽样分布( 个容量为 的样本均值的分布即为样本均值的抽样分布)

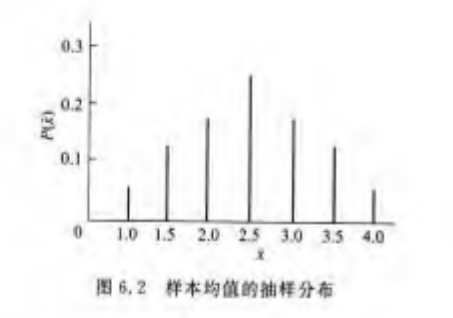
2. 样本统计量的抽样分布
为了抽象出针对不同事物的不同量纲的抽样分布间存在的规律,我们总结出了不同样本统计量的抽样分布趋于的分布形状。
样本均值的抽样分布
正态分布
中心极限定理 (central limit theorem):
若总体分布非正态分布,随着样本容量 的增大,单个总体参数推断时样本均值的抽样分布趋于正态分布。
若总体分布为正态分布,则无论样本容量大小,样本均值的抽样分布均为正态分布。
即从满足 的总体中抽取容量为 的随机样本时,样本均值 的抽样分布近似于 。
t分布
分布 (t-distribution):
服从正态分布的总体,样本均值 的抽样分布服从正态分布(中心极限定理)。其样本均值经标准化后服从自由度为 的 分布。因此单个总体参数推断时样本均值的抽样分布满足:
分布的性质
-
随着自由度的增大,分布趋近于正态分布
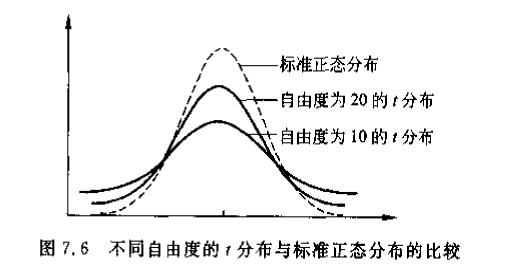
样本方差的抽样分布
卡方分布
卡方分布 (Chi-Square Distribution):
个独立的标准正态分布变量的平方和服从自由度为 的卡方分布。
单个总体参数推断时样本方差的抽样分布满足:
卡方分布的性质
-
卡方分布的期望为 ,方差为
-
卡方分布具有可加性,若 ,,则随机变量 服从 。
-
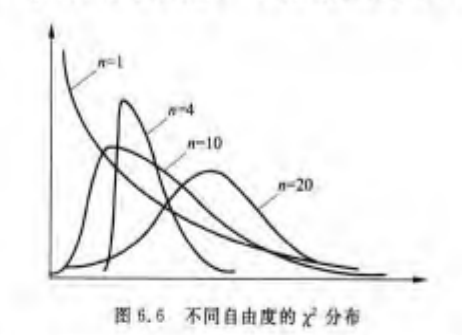
卡方分布的形状取决于自由度 (样本容量)的大小,随着自由度的增大趋于对称。
两个样本方差比的抽样分布
F分布
分布 (t-distribution):
是服从自由度为 的 分布的随机变量,;
是服从自由度为 的 分布的随机变量,。
则其服从自由度为 的 分布:
两个总体参数推断时样本方差比的抽样分布满足:
3. 点/区间估计
统计推断 (statisticl inference)是通过样本推断总体的统计方法,包括参数估计(由样本统计量估计总体统计量)和假设检验(对总体参数作出假设并判断假设是否成立)。
相关概念
参数估计 (parameter estimation)
用样本统计量估计总体参数,总体参数记作
估计量 (estimator)
用来估计总体参数的统计量,记作
估计值 (estimate)
用来估计总体参数时计算得到的的估计量的具体数值
参数估计的方法有两种:
-
点估计 (point estimate)
用样本估计量 的值(估计值)直接作为总体参数 的估计得到的值
-
区间估计 (interval estimate)
在点估计的基础上,给出估计值的浮动范围(如 ),作为总体参数 估计存在的区间
为了度量估计可靠性,有以下概念:
-
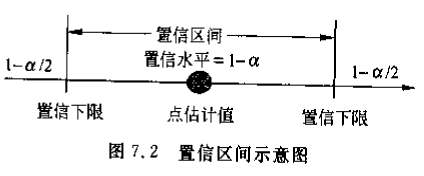
置信区间 (confidence interval)
区间估计中,体参数 估计存在的区间为置信区间(总体参数落在置信区间的概率是 )
-
置信水平/置信系数 (confidence level)
将构造置信区间的步骤重复多次,置信区间中包
含总体参数 真实值的次数所占的比率如果用某种方法构造的所有区间(不同抽样中得到的)中有 的区间包含总体参数的真实值, 的区间不包含总体参数的真实值。那么用该方法构造的区间称为置信水平为 的置信区间。
总体均值的区间估计
graph LR;
0[均值] --- 1[大样本] ---> a[正态分布];
0 --- 2[小样本] --- 已知方差的正态总体 ---> a;
2 --- 未知方差的正态总体 ---> t分布

正态分布的区间估计
条件:
大样本 或 已知总体方差且总体正态分布的小样本
步骤:
- 计算样本估计量
2. 计算置信区间(置信上下限为 )

其中, 为样本容量;标准正态分布的 分位数可查表得到; 为总体的标准差,在大样本中可用样本的标准差 替代。
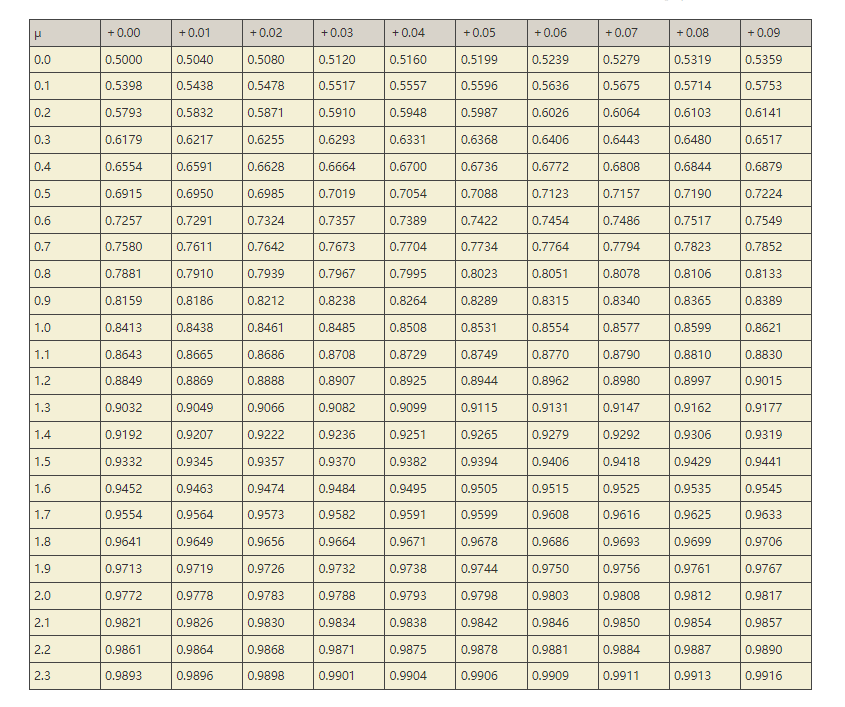
标准正态分布查表
-
查概率
案例1:若有 ,求
-
标准化得 ,因此正态分布的概率问题可以转化为标准正态分布 中求 。
-
标准正态分布表纵轴为变量 得整数及一位小数部分,横轴为其二位小数部分,横纵轴对应索引值为 。
因此 为 处的值。
-
-
查 分位数
案例2:求
-
代表标准正态分布曲线中右侧面积为 时 的值,求 即求 时的 。
-
因此 。
由值找坐标得 ,因此 的值为 。
-
例题

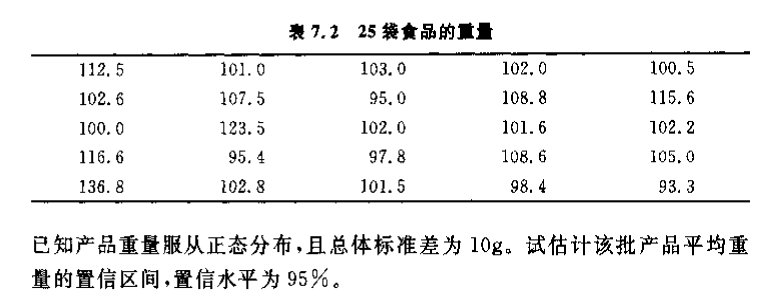
满足条件:已知总体方差且总体正态分布的小样本
-
计算样本均值:
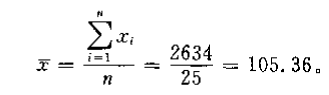
-
计算置信区间:
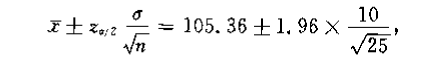
-
得到结果:
该食品平均重量在 置信水平下的置信区间为 。
t分布的区间估计
条件:
未知总体方差且总体正态分布的小样本
步骤:
- 计算样本估计量
2. 计算置信区间(置信上下限为 )
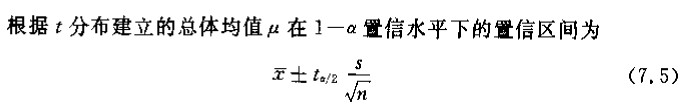
其中, 为样本容量; 分布的 分位数可查表得到; 为样本的标准差。
t分布查表

- 临界值
案例1:求
- t$$ 分布表**纵轴为自由度$n$ ,横轴为单尾/双尾时分位点,横纵轴对应索引值为 $t$临界值**。 因此 $(双尾0.05/单尾0.025,15)$ 处值为 $t$临界值 $2.131$。
例题

满足条件:未知总体方差且总体正态分布的小样本
-
计算样本均值:
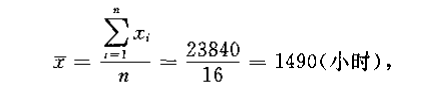
计算样本标准差:
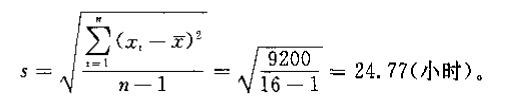
-
计算置信区间:
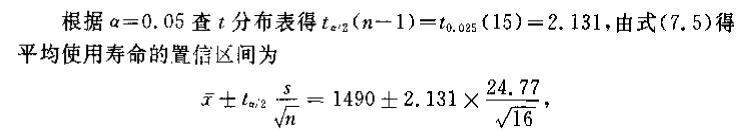
得到结果:

4. 极大似然估计
5. 贝叶斯估计
参考资料
- 《统计学》贾俊平
- 《概率论与数理统计》茆诗松
- 通俗统计学之t分布的区间估计-bilibili
- 标准正态分布查表
- 利用标准正态分布表查询概率和分位点
待补充部分:
- 中心极限定理,分布,分布,分布的证明及详情
- 样本比例、两个样本均值差、两个样本比例差满足的抽样分布及证明
- 总体比例的区间估计,两个总体参数的区间估计
、
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
