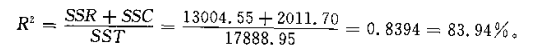统计学(四) 方差分析
本文最后更新于:2023年2月28日 下午
1. 相关概念
方差分析 (analysis of variance, ANOVA)
通过检验多个总体均值是否相等判断分类型自变量对数值型因变量是否有显著影响
检验数据以分类型数据为自变量,数值型数据为因变量
以“不同行业对投诉次数是否有影响”进行方差分析
因素/因子 (factor)
方差分析中所要检验的对象
“行业”即为因子
水平/处理 (treatment)
因素的不同表现
“零售业”、“旅游业”、“家电制造业”等是因子的水平
基本思想
-
方差分析是通过对数据误差来源的分析来判断不同总体的均值是否相等,进而分析自变量对因变量是否有影响。
数据的误差有随机误差(抽样的随机性造成的)、系统误差(系统性因素,在这里为因子对不同水平的影响),通过平方和 (sum of squares) 衡量
因子的同一水平下样本的误差为组内误差 (within groups) ,只含随机误差
因子的不同水平间样本的误差为组间误差 (within groups) ,含随机误差和系统误差
我们通过比较组内误差和组间误差度量系统误差,判断因子对不同水平是否有显著影响
-
方差分析建立在假设检验的基础上,可以解决假设检验无法同时对多个总体进行检验的问题
基本步骤:提出假设 -> 构造检验的统计量 -> 统计决策
前提条件
- 因子的每一个水平都满足正态分布
- 因子的每一个水平方差相等
- 因子的每一个水平观测值相互独立
2. 单因素方差分析
单因素方差分析 (one-way analysis of variance)
方差分析中只涉及一个分类型自变量(只有一个因子)
- 分布与临界值
- 关系强度
数据结构
以“不同行业对投诉次数是否有影响”为例:
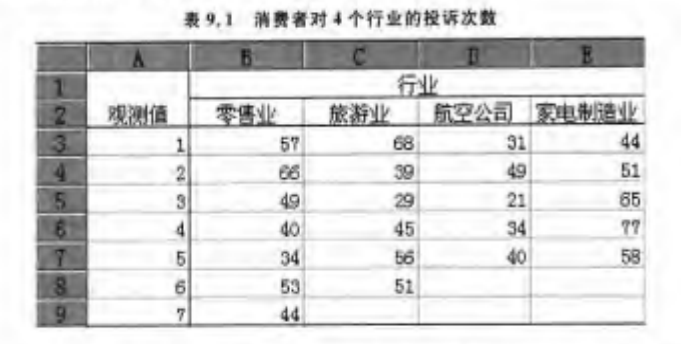
因此,单因素方差分析的数据结构中横轴表示因子的各水平,纵轴表示观测值序号。 表示第 个水平的第 个观测值:
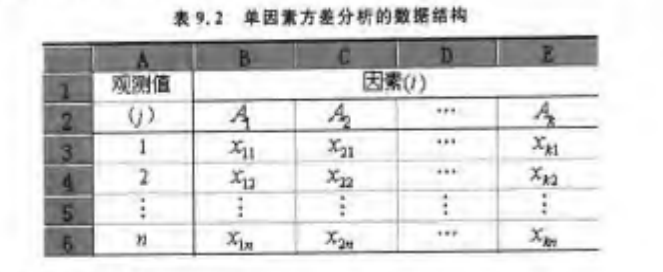
分析步骤
-
提出假设

本例的假设:

-
构造检验统计量
类均值
总平均值 /各水平平均值
本例中,以零售业 为例:

最终结果为:
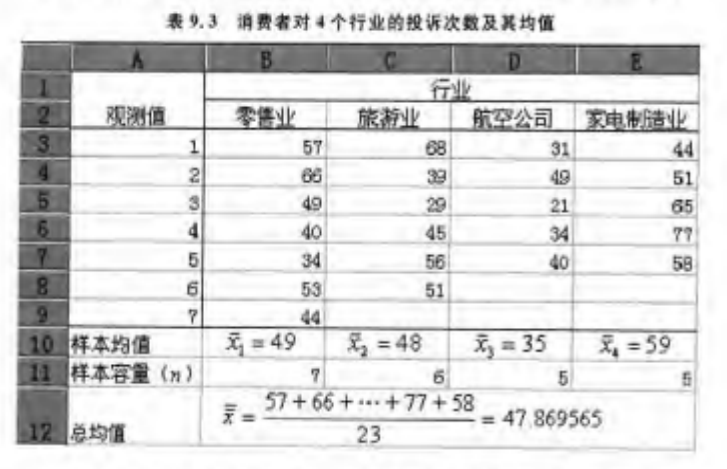
个误差平方和 (sum of squares)
-
总误差平方和 (sum of squares for total, SST)
全部观测值 与总平均值 的误差平方和
本例中,有:
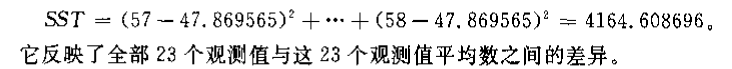
-
水平项误差平方和 (sum of squares for factor A, SSA)
各水平平均值 与总平均值 的误差平方和,反映各水平总体的样本均值间差异程度,又称组间平方和
本例中,有:

-
误差项平方和 (sum of squares for error, SSE)
每个水平组内观测值 与其组平均值 的误差平方和之和,反映每个水平组内观测值离散状况,又称组内平方和/残差平方和
-
个误差平方和间关系
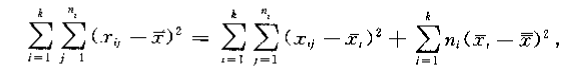
- 度量随机误差和系统误差,也称自变量效应/因子效应
- 度量随机误差,也称残差效应
- 度量总误差,反映自变量和残差变量的共同影响
个均方 (mean square)
为消除各水平样本容量对误差平方和的影响,将误差平方和与自由度相比得到均方。
比较, 的均方 , 的差异大小,即可得到系统误差的大小。

-
组间均方 ()

本例中,有:
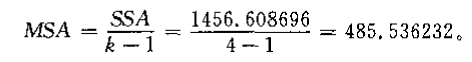
-
组内均方()

本例中,有:
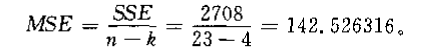
检验统计量
为 , 之比。当 为真时,满足分子自由度、分母自由度 的 分布
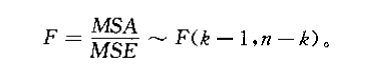
-
-
统计决策
将统计量的值 与给定的显著性水平 的临界值 比较
在 分布查找分子自由度 ,分母自由度 时的临界值
- 选取分位数 对应的表
- 查找分子、分母自由度对应的索引值
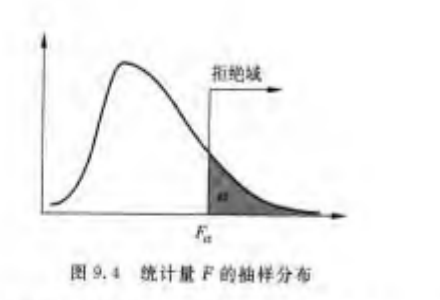
- ,拒绝原假设
- ,不能拒绝原假设
以上过程可通过方差分析表 (analysis of variance table) 清晰展示:
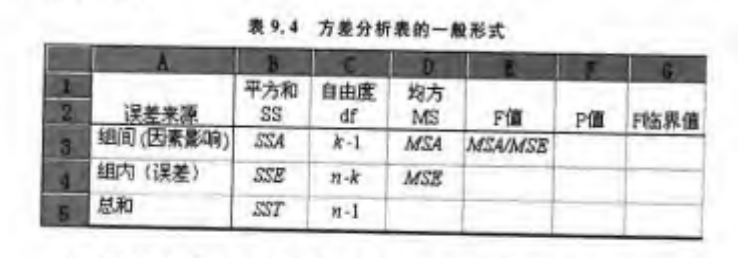
个关系强度
自变量平方和 占总平方和 的比例大小反映自变量和因变量间的关系强度(正比)
因此,行业(自变量)对投诉次数(因变量)的影响效应占总效应的 ;其他因素(残差变量)占
3. 双因素方差分析
双因素方差分析 (two-way analysis of variance)
方差分析中涉及两个分类型自变量(两个因子),是检验两个因子自变量对数值因变量的影响
无交互作用的双因素方差分析
两个因子相互独立
- 分布 与临界值
- 关系强度
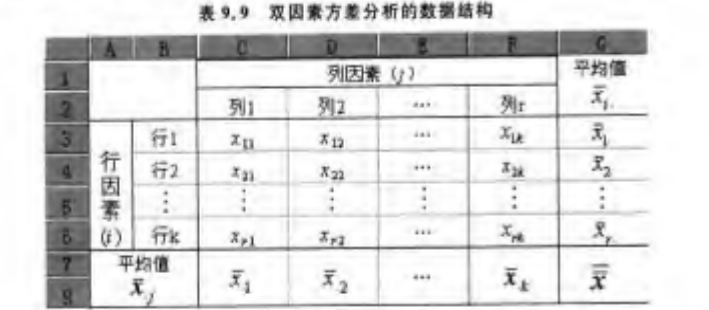
数据结构
以“不同品牌的彩电在各地区的销售量数据”为例
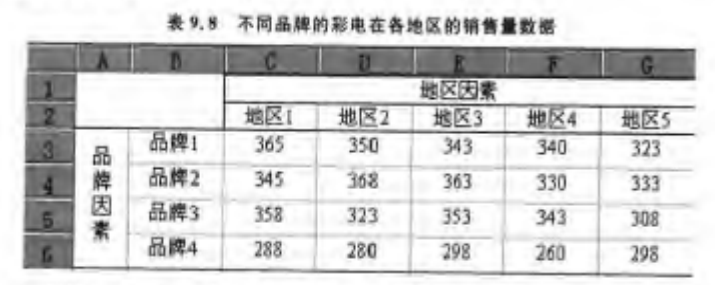
因此,横轴表示列因素的 个水平,竖轴表示行因素的 个水平。 表示第 个行因素水平、第 个列因素水平的观测值。
分析步骤
-
提出假设
需要对行、列因子分别提出假设


本例中有:

-
构造检验统计量
类均值
-
行因素第 个水平观测值的平均值 / 列因素第 个水平观测值的平均值 / 全部 个观测值的总平均值
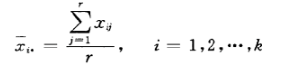
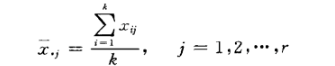
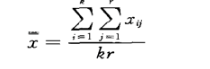
个误差平方和 (sum of squares)
-
总误差平方和 (sum of squares for total, SST)
全部观测值 与总平均值 的误差平方和
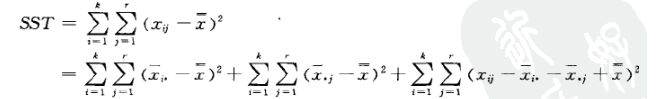
-
行因素误差平方和 (sum of squares for raw, SSR)
行因素各水平观测值的平均值 与总平均值 的误差平方和
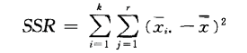
-
列因素误差平方和 (sum of squares for column, SSC)
列因素各水平观测值的平均值 与总平均值 的误差平方和
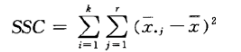
-
随机误差平方和 (sum of squares for error, SSE)
除行因素和列因素之外的剩余因素影响产生的误差平方和
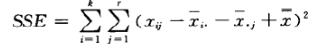
-
个误差平方和间关系
个均方 (mean square)

-
行因素的均方
-
列因素的均方
-
随机误差项的均方
检验统计量
当 为真时,与之比 满足分子自由度为自由度、为自由度 的 分布

-
-
统计决策
将统计量的值 与给定的显著性水平 的临界值 比较
行因素
- ,拒绝原假设
- ,不能拒绝原假设
列因素
- ,拒绝原假设
- ,不能拒绝原假设
在 分布查找对应分子自由度 ,分母自由度 时的临界值
- 选取分位数 对应的表
- 查找分子、分母自由度对应的索引值

以上过程可通过方差分析表 (analysis of variance table) 清晰展示:
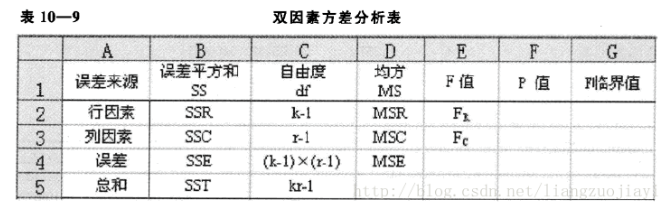
个关系强度
两个自变量对因变量的联合效应与总平方和的比值为关系强度
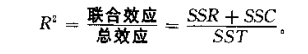
本例中,有:
因此,品牌因素和地区因素的联合效应占总效应的 ,其他因素(残差效应)仅占 ,品牌因素和地区因素的联合与销售量有较强关系
有交互作用的双因素方差分析
两个因子有交互作用
数据结构
以“路段、时段、路段和时段的交互作用对行车时间的影响”为例
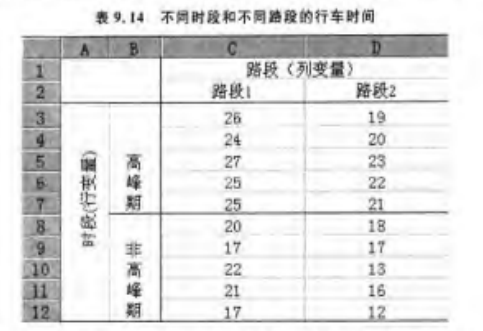
因此,横轴表示列因素的 个水平,竖轴表示行因素的 个水平,每一个水平的行数为 。 表示第 个行因素水平、第 个列因素水平的 个观测值。
分析步骤
-
提出假设
和无交互作用时一样
-
构造检验统计量
类均值
- 行因素第 个水平观测值的平均值
- 列因素第 个水平观测值的平均值
- 行因素第 个水平、列因素第 个水平中所有观测值均值
- 全部 个观测值的总平均值
个误差平方和 (sum of squares)
个误差平方和间关系
可通过方差分析表 (analysis of variance table) 清晰展示:
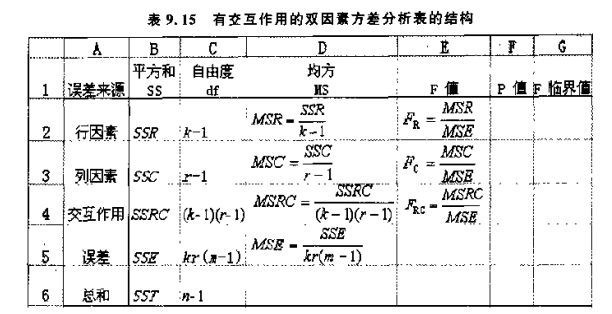
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!